IME - CG - Geometria

por PedroCunha Dom 22 Dez 2013, 11:43

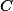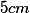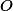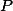Considere um circulo $IME - CG - Geometria Mathtex$ de raio $IME - CG - Geometria Mathtex$ com centro $IME - CG - Geometria Mathtex$ em $IME - CG - Geometria Mathtex$ e um ponto $IME - CG - Geometria Mathtex$ sobre a circunferência deste circulo. Seja 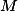$IME - CG - Geometria Mathtex$ a projeção do ponto 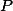$IME - CG - Geometria Mathtex$ sobre o eixo 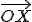$IME - CG - Geometria Mimetex$ . Determine a equação do lugar geométrico do centro de gravidade do triângulo 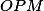$IME - CG - Geometria Mathtex$ , quando 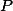$IME - CG - Geometria Mathtex$ se desloca sobre a circunferência do circulo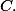 $IME - CG - Geometria Mathtex.cgi?C$

Alguém pode ajudar?

Att.,
Pedro

por **Medeiros** Dom 22 Dez 2013, 12:01

Só um detalhe, Pedro. Parece-me, pelo seu desenho do círculo inscrito, que você marcou CG no encontro das bissetrizes (incentro). Mas o centro de gravidade fica no encontro das medianas (baricentro).

A figura que resulta é uma elipse de traços no primeiro quadrante (2r/3, 0) e (0, r/3), onde r=5cm.

por PedroCunha Dom 22 Dez 2013, 15:35

Poderia me explicar como você concluiu isso?

(Entendi quanto ao desenho)

Abraço

por **Euclides** Dom 22 Dez 2013, 16:53

Não tenho uma solução analítica mas encontrei uma solução gráfica que permite visualização.

por **Medeiros** Dom 22 Dez 2013, 17:38

Boa tarde Pedro! Vou tentar.

G é baricentro (encontro das medianas) do triângulo OPM.
Então:
PJ = JM = PM/2
OK = KM = OM/2

PM = r.sen(alfa) -----> JM = (r/2).sen(alfa)

OM = r.cos(alfa) -----> KM = (r/2).cos(alfa)

eq. da reta s

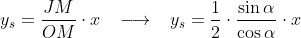
$y_s=\frac{JM}{OM}\cdot x \;\;\; \longrightarrow \;\;\; y_s=\frac{1}{2}\cdot \frac{\sin \alpha }{\cos \alpha }\cdot x$

eq. da reta t

$\\ y_t=\frac{PM}{KM}\cdot \left (x-OK \right ) \;\;\; \longrightarrow \;\;\; y_t=\frac{r.\sin \alpha}{\frac{r}{2}\;\cos \alpha}\left(x-\frac{r.\cos \alpha}{2} \right )\\\\ y_t=2 \cdot \frac{\sin \alpha}{\cos \alpha} \cdot x-r.\sin \alpha$

ponto G

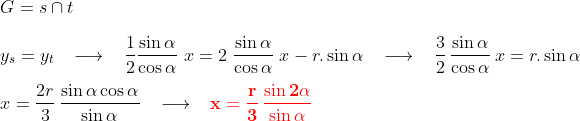
$\\ G=s\cap t\\\\ y_s = y_t \;\;\;\longrightarrow\;\;\; \frac{1}{2} \frac{\sin \alpha}{\cos \alpha}\;x=2\;\frac{\sin \alpha}{\cos \alpha}\;x-r.\sin \alpha \;\;\;\longrightarrow\;\;\; \frac{3}{2}\,\frac{\sin \alpha}{\cos \alpha}\,x=r. \sin \alpha \\\\ x=\frac{2r}{3}\,\frac{\sin \alpha \cos \alpha}{\sin \alpha} \;\;\;\longrightarrow\;\;\; {\color{Red} \mathbf{x=\frac{r}{3}\,\frac{\sin 2\alpha}{\sin \alpha}}}$

levando este valor na eq. de y_s,

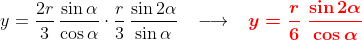
$\\ y=\frac{2r}{3}\,\frac{\sin \alpha}{\cos \alpha} \cdot \frac{r}{3}\,\frac{\sin 2\alpha}{\sin \alpha} \;\;\;\longrightarrow\;\;\; {\color{Red} \boldsymbol{y=\frac{r}{6}\;\frac{\sin 2\alpha}{\cos \alpha}}}$

Em vermelho temos as coordenadas do ponto G em função do ângulo alfa que varia conforme o deslocamento do ponto P sobre a circunferência C.
Basta-nos dar valores a alfa, para verificar o deslocamento de D. Foi o que fiz para alguns pontos -- assinalados no desenho acima.
Evidentemente quando o ponto P está sobre os eixos coordenados, o triângulo deixa de existir (se "desfaz"), não existindo o G. Neste caso, calculamos o limite para alfa=0º e alfa=90º.

p/ alfa=0º
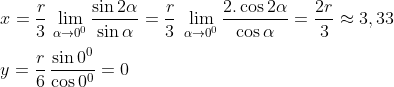
$\\ x=\frac{r}{3}\,\lim_{\alpha \rightarrow 0^0} \frac{\sin2\alpha}{\sin \alpha}=\frac{r}{3}\;\lim_{\alpha \rightarrow 0^0} \frac{2.\cos 2\alpha}{\cos \alpha}=\frac{2r}{3}\approx 3,33 \\\\ y=\frac{r}{6}\, \frac{\sin 0^0}{\cos 0^0}=0$

p/ alfa=90º
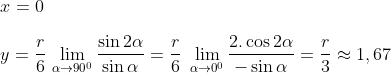
$\\ x=0 \\\\ y=\frac{r}{6}\,\lim_{\alpha \rightarrow 90^0} \frac{\sin2\alpha}{\sin \alpha}=\frac{r}{6}\;\lim_{\alpha \rightarrow 0^0} \frac{2.\cos 2\alpha}{-\sin \alpha}=\frac{r}{3}\approx 1,67$

p/ alfa=30º
x = r√3/3 ≈ 2,89
y = r/6 ≈ 0,83

p/ alfa = 45º
x = r√2/3 ≈ 2,36
y = r√2/6 ≈ 1,18

p/ alfa = 60º
x = r/3 ≈ 1,67
y = r√3/6 ≈ 1,44

p/ alfa = 75º
x ≈ 0,86
y ≈ 1,61

p/ alfa = 85º
x ≈ 0,29
y ≈ 1,66

Bem, Pedro, foi isso que fiz. Talvez de posse das coordenadas do ponto G você possa levantar a equação da curva fazendo alfa variar de 0 até 2pi.

Abs.

por **Medeiros** Dom 22 Dez 2013, 17:50

Maravilha de gráfico, Euclides!
Mas me diz, como você achou a eq. da elipse?

por **Euclides** Dom 22 Dez 2013, 18:08

Medeiros escreveu:Maravilha de gráfico, Euclides!
Mas me diz, como você achou a eq. da elipse?

Medeiros,

muito bom foi o seu trabalho. Com os dois limites você encontrou os dois semi-eixos da elipse

$a=\frac{10}{3}\;\;\;\;\;\;\;\;\;\;b=\frac{5}{3}$

que eu encontrei apenas graficamente. A animação do Geogebra me mostrou que era uma elipse (na verdade só poderia ser ou uma elipse, ou uma circunferência). De posse da natureza da curva e dos semi eixos foi fácil:

$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$