PUC( 1998)

Seja 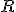 um retângulo que tem  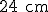de perímetro. Unindo-se sucessivamente os pontos médios dos lados de  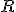obtém-se um losango. Qual deve ser a medida do lado desse losango para que sua área seja máxima?

GAB: 3 √ 2 cm

gabrieldavid escreveu:Seja  um retângulo que tem  de perímetro. Unindo-se sucessivamente os pontos médios dos lados de  obtém-se um losango. Qual deve ser a medida do lado desse losango para que sua área seja máxima?

GAB: 3 √ 2 cm

Bom dia, gabrieldavid

Para que a área desse losango seja máxima, também máxima deverá ser a área do retângulo que o originou.
Calculando a medida dos lados do retângulo para que sua área seja máxima:
a,b = lados do retângulo
2(a+b) = 24
a+b = 24/2
a+b = 12
b = 12-a

S = ab = a(12-a) 
S = -a² + 12a

O gráfico de S é o de uma parábola, com concavidade voltada para baixo (coeficiente de a² é negativo), indicando ter ela valor máximo em seu vértice.
Coordenadas do vértice:
S = -a² + 12a
Av = -12/-2 = 6 
Sv =-6² + 12*6 = -36 + 72 = 36 

Essas são a medida do lado (6) e da área do retângulo (36), indicando que esse retângulo deverá ter seus lados iguais sendo, portanto, um quadrado de lados medindo 6 cm cada um.
Sendo assim, o lado do losango nele inscrito, tendo como vértices os pontos médios desse retângulo quadrado, deverá medir:
L² = (a/2)² + (a/2)² 
L² = (6/2)² + (6/2)²
L² = 2*3²
L = √(2*3²)
L = 3√2 cm




Um abraço

Bom dia, Mestre Ivomilton, muito obrigado pela explicação.Grande abraço!