(PUC-RJ) Soma de potências de i

Seja i o número complexo (0;1). Então, a soma: 


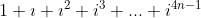
a) é um imaginário puro
b) é um real positivo
c) é real se e só se n é impar
d) é uma potência inteira de i
e) é nula

gabarito:

i^0 = 1
i^1 = I
i^2 = -1
i^3 = -i

Os resultados repetem- se de 4 em 4
Complete.

Apenas complementando, é bom ressaltar que o complexo (0, 1) é nada mais nada menos do que a própria unidade imaginária i. (z = a + bi, se a = 0 e b = 1, então z = i).

Para finalizar a questão você tem que perceber que "4n - 1" equivale ao número antecessor à quantidade de termos da soma. Se por exemplo o último termo for i ^ 7, o número 7 é o número antecessor à quantidade de termos da soma que será 8.

Como posso descobrir a soma total? Se puderem, por favor me ajudem pois não sei como resolver.

Minha tentativa foi a seguinte: Tomei como premissa de que todos os termos iriam zerar, sobrando apenas o ultimo termo, que é i^(4n-1)

Depois, fiz a análise do n para valores ímpares e pares. 
Deu certo, porém eu aceitei como verdade que a soma dos termos seriam zero, o que não é correto, pois não sei aonde a contagem acaba, nem se a contagem terminará em valor par ou ímpar. Há alguma forma de resolver a parte do somatório?

Elcioschin escreveu:i^0 = 1
i^1 = I
i^2 = -1
i^3 = -i

Os resultados repetem- se de 4 em 4
Complete.

A sequência é:

i^0 + i^1 + i^2 + i^3 + ... + i^(4n - 1)

Como eu disse ali em cima, "4n - 1" representa a quantidade de termos da soma - 1, portanto, a quantidade de termos da soma é 4n. Se n = 1, existiram 4 termos, portanto a soma será 0. Se n = 2, existiram 8 termos, que de 4 em 4 vão somar zero do mesmo jeito.

Acredito que você tenha dúvida sobre as potências de i.

O Elcioschin já fez a sequência de i ^ 0 até i ^ 3, vou fazer agora de i ^ 4 até i ^ 7:

i ^ 4 = i ^ 3 * i  = 1
i ^ 5 = i ^ 4 * i  = i
i ^ 6 = i ^ 5 * i  = -1
i ^ 7 = i ^ 6 * i  = -i

Esse padrão das potências (1, i, -1, -i) se repete infinitamente. Observe que esses 4 valores somados dão 0.

Essa parte eu consegui entender, eles se anulam de 4 em 4 termos.
Então, você apenas atribuiu um valor ímpar e um valor par pra confirmar que zeraria?

Não importa se (n) é ímpar ou par, o que importa é que a quantidade de termos (4n) é um número múltiplo de 4. Ou seja, vamos ter n grupos de 4 potências sendo somadas, que como já vimos, cada grupo tem valor total igual a 0.