Demonstrando a sequência de Fibonacci
3 participantes
PiR2 :: Recursos extras :: Demonstrações
Página 1 de 1
Demonstrando a sequência de Fibonacci
por Nina Luizet Sab 15 Ago 2015, 19:50
Graficamente, temos que :
Quando possível, faço um tópico demonstrando as fórmulas das progressões.
Nina Luizet- matadora
- Mensagens : 1215
Data de inscrição : 21/06/2014
Idade : 23
Localização : Brasil, RN , Mossoró
Demonstração do termo geral
por Ashitaka Sab 15 Ago 2015, 21:26
____________________________________________
"Now it's three in the morning and you're eating alone
Look around, there's no one else left"
Ashitaka- Monitor
- Mensagens : 4358
Data de inscrição : 12/03/2013
Localização : São Paulo
Re: Demonstrando a sequência de Fibonacci
por Willian Honorio Dom 18 Mar 2018, 15:04
Um resultado bastante interessante provindo desta fórmula:
Escrevamos a Sequência de Fibonacci:
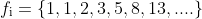
E façamos razões entre termos consequentes e subsequentes desta sequência:
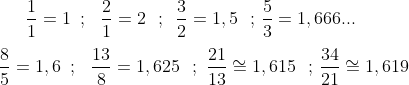
Percebe-se que quanto maior o termo de ordem n+1 por um de ordem n as razões tendem a um certo número... Utilizando a Fórmula de Binet para a Sequência de Fibonacci, faremos a razão entre um termo qualquer de ordem n+1 por um de ordem n:
^{n+1}-\left&space;(&space;\frac{1-\sqrt{5}}{2}&space;\right&space;)^{n+1}&space;\right&space;]}{\frac{1}{\sqrt{5}}\left&space;[&space;\left&space;(\frac{1+\sqrt{5}}{2}&space;\right&space;)^{n}-\left&space;(&space;\frac{1-\sqrt{5}}{2}&space;\right&space;)^{n}&space;\right&space;]} "x=\frac{\frac{1}{\sqrt{5}}\left [ \left ( \frac{1+\sqrt[]{5}}{2} \right )^{n+1}-\left ( \frac{1-\sqrt{5}}{2} \right )^{n+1} \right ]}{\frac{1}{\sqrt{5}}\left [ \left (\frac{1+\sqrt{5}}{2} \right )^{n}-\left ( \frac{1-\sqrt{5}}{2} \right )^{n} \right ]}")
Tomando um n tão grande quanto se queira, teremos o limite:
^{n+1}-\left&space;(&space;\frac{1-\sqrt{5}}{2}&space;\right&space;)^{n+1}&space;\right&space;]}{\frac{1}{\sqrt{5}}\left&space;[&space;\left&space;(\frac{1+\sqrt{5}}{2}&space;\right&space;)^{n}-\left&space;(&space;\frac{1-\sqrt{5}}{2}&space;\right&space;)^{n}&space;\right&space;]}\\\\a=\frac{1+\sqrt{5}}{2}\\\\b=\frac{1-\sqrt{5}}{2}\\\\\therefore&space;\\x=\lim_{n\rightarrow&space;+\infty}\frac{a^{n+1}-b^{n+1}}{a^{n}-b^{n}} "x=\lim_{n\rightarrow +\infty}\frac{\frac{1}{\sqrt{5}}\left [ \left ( \frac{1+\sqrt[]{5}}{2} \right )^{n+1}-\left ( \frac{1-\sqrt{5}}{2} \right )^{n+1} \right ]}{\frac{1}{\sqrt{5}}\left [ \left (\frac{1+\sqrt{5}}{2} \right )^{n}-\left ( \frac{1-\sqrt{5}}{2} \right )^{n} \right ]}\\\\a=\frac{1+\sqrt{5}}{2}\\\\b=\frac{1-\sqrt{5}}{2}\\\\\therefore \\x=\lim_{n\rightarrow +\infty}\frac{a^{n+1}-b^{n+1}}{a^{n}-b^{n}}")
Utilizando a fatoração demonstrada no código ao lado: Fatoração
(a^{n}+b.a^{n-1}+...+b^{n})\\a^{n}-b^{n}=(a-b)(a^{n-1}+b.a^{n-2}+...+b^{n-1})\\\\x=\lim_{n\rightarrow&space;+\infty}\frac{(a-b)(a^{n}+b.a^{n-1}+...+b^{n})}{(a-b)(a^{n-1}+b.a^{n-2}+...+b^{n-1})}\\\\x=\lim_{n\rightarrow&space;+\infty}\frac{(a^{n}+b.a^{n-1}+...+b^{n})}{(a^{n-1}+b.a^{n-2}+...+b^{n-1})}\\\\ "a^{n+1}-b^{n+1}=(a-b)(a^{n}+b.a^{n-1}+...+b^{n})\\a^{n}-b^{n}=(a-b)(a^{n-1}+b.a^{n-2}+...+b^{n-1})\\\\x=\lim_{n\rightarrow +\infty}\frac{(a-b)(a^{n}+b.a^{n-1}+...+b^{n})}{(a-b)(a^{n-1}+b.a^{n-2}+...+b^{n-1})}\\\\x=\lim_{n\rightarrow +\infty}\frac{(a^{n}+b.a^{n-1}+...+b^{n})}{(a^{n-1}+b.a^{n-2}+...+b^{n-1})}\\\\")
Que é o limite de um polinômio racional em ''a'', com ''b'' como coeficientes. Sendo o polinômio racional com n tendendo ao infinito, o termo de ordem n do numerador cresce muito mais que os outros deste mesmo polinômio nos quais poderão ser desprezados. No denominador, o termo de ordem n-1 cresce muito mais que os outros deste mesmo polinômio nos quais poderão ser desprezados. O limite é, por conseguinte:
}=\lim_{n\rightarrow&space;+\infty}a=a\\\therefore&space;\\x=\boxed{\phi&space;=\frac{1+\sqrt{5}}{2}} "x=\lim_{n\rightarrow +\infty}\frac{a^{n}}{a^{n-1}}=\frac{\infty}{\infty}\,\,\,!!!\\\\x=\lim_{n\rightarrow +\infty}a^{n-(n-1)}=\lim_{n\rightarrow +\infty}a=a\\\therefore \\x=\boxed{\phi =\frac{1+\sqrt{5}}{2}}")
Que é o notável Número de Ouro da proporção áurea, muito presente na natureza. Ou seja, razões entre números na Sequência de Fibonacci tendem ao Número de Ouro, num valor mais usual:
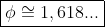
Escrevamos a Sequência de Fibonacci:
E façamos razões entre termos consequentes e subsequentes desta sequência:
Percebe-se que quanto maior o termo de ordem n+1 por um de ordem n as razões tendem a um certo número... Utilizando a Fórmula de Binet para a Sequência de Fibonacci, faremos a razão entre um termo qualquer de ordem n+1 por um de ordem n:
Tomando um n tão grande quanto se queira, teremos o limite:
Utilizando a fatoração demonstrada no código ao lado: Fatoração
Que é o limite de um polinômio racional em ''a'', com ''b'' como coeficientes. Sendo o polinômio racional com n tendendo ao infinito, o termo de ordem n do numerador cresce muito mais que os outros deste mesmo polinômio nos quais poderão ser desprezados. No denominador, o termo de ordem n-1 cresce muito mais que os outros deste mesmo polinômio nos quais poderão ser desprezados. O limite é, por conseguinte:
Que é o notável Número de Ouro da proporção áurea, muito presente na natureza. Ou seja, razões entre números na Sequência de Fibonacci tendem ao Número de Ouro, num valor mais usual:
Willian Honorio- Matador
- Mensagens : 1271
Data de inscrição : 27/04/2016
Idade : 26
Localização : São Paulo
Tópicos semelhantes» Demonstrando as fórmulas das progressões
» Demonstrando as fórmulas da Gravitação
» 8 Fibonacci
» 8 Fibonacci
» 9 fibonacci
» Demonstrando as fórmulas da Gravitação
» 8 Fibonacci
» 8 Fibonacci
» 9 fibonacci
PiR2 :: Recursos extras :: Demonstrações
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos|
|
|
