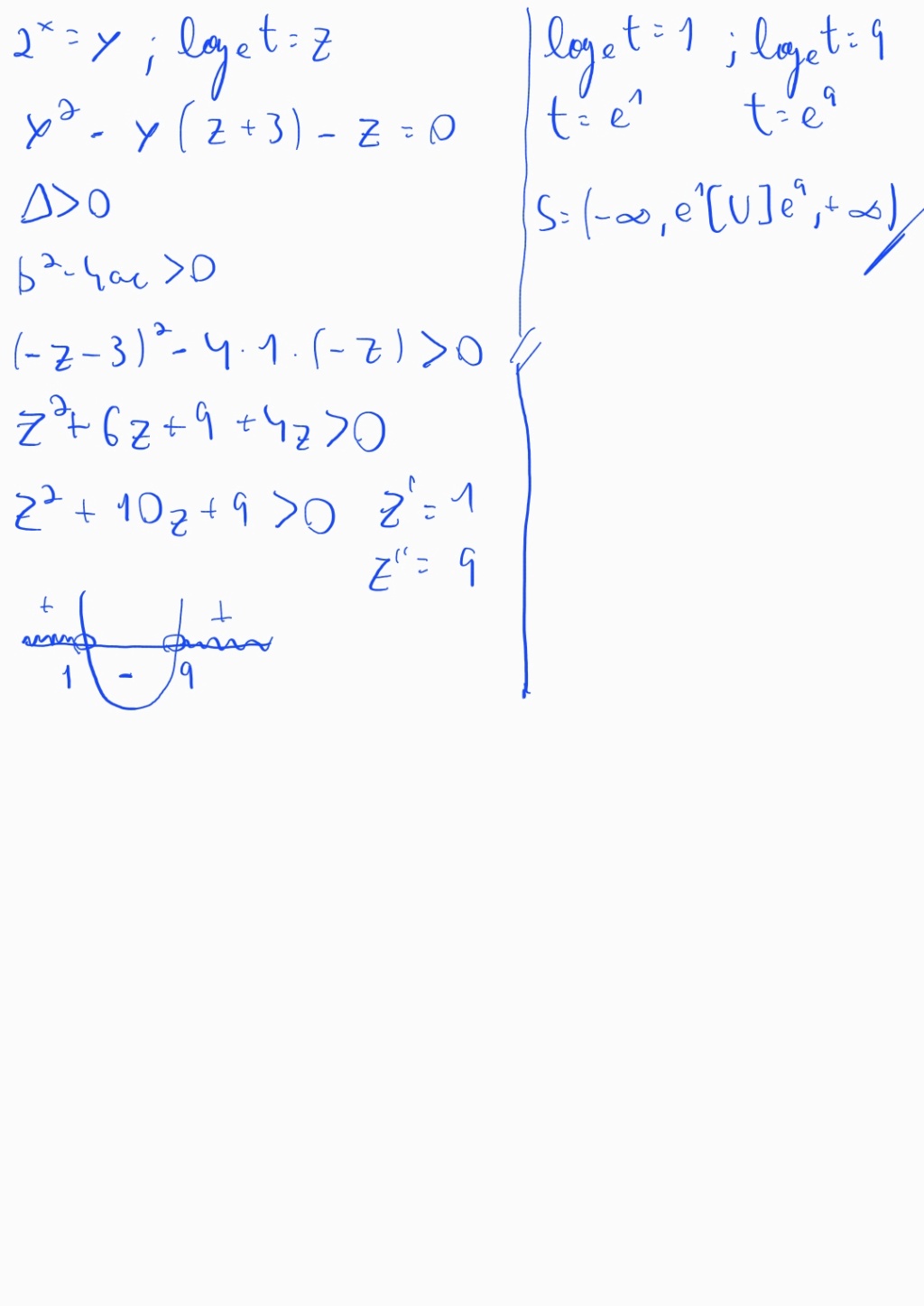Função Logaritmica
5 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 2
Página 1 de 2 • 1, 2 
 Função Logaritmica
Função Logaritmica
Determine o valor de t para que a equação 4x - (loge t + 3) 2x - loge t = 0 admita duas raízes reais e distintas
Gabarito:
0e-1
Minha resolução:
2x = y e loge t = ln t
y2- (loge t + 3) y - loge t = 0
com y>0
Para ter duas raízes distintas Δ>0
ln2t + 9 +6ln t -4*-ln t >0
trocando ln t por r:
r2 +10r + 9 > 0
r<-9 ou r >-1
mas como y > 0; as raízes devem ser positivas:
Soma > 0 e Produto >0
Ln t < -3 e Ln t > 0
então r<-1 é descartado
ln t <-9
00??[/size]
Gabarito:
0e-1
Minha resolução:
2x = y e loge t = ln t
y2- (loge t + 3) y - loge t = 0
com y>0
Para ter duas raízes distintas Δ>0
ln2t + 9 +6ln t -4*-ln t >0
trocando ln t por r:
r2 +10r + 9 > 0
r<-9 ou r >-1
mas como y > 0; as raízes devem ser positivas:
Soma > 0 e Produto >0
Ln t < -3 e Ln t > 0
então r<-1 é descartado
ln t <-9
00??[/size]
Última edição por vinimasa72 em Qui 03 Ago 2023, 20:28, editado 2 vez(es) (Motivo da edição : correção de erros de digitação)
vinimasa72- Padawan

- Mensagens : 52
Data de inscrição : 20/03/2023
Idade : 19
Localização : Jundiai SP

Alien supremo- Jedi

- Mensagens : 438
Data de inscrição : 20/08/2022
Idade : 22
Localização : Rio de Janeiro
 Re: Função Logaritmica
Re: Função Logaritmica
z² + 10.z + 9 = 0
As raízes y = 1 e y = 9 não estão corretas: as raízes corretas são y = -9 e y = -1
As raízes y = 1 e y = 9 não estão corretas: as raízes corretas são y = -9 e y = -1

Elcioschin- Grande Mestre

- Mensagens : 73172
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
 Re: Função Logaritmica
Re: Função Logaritmica
Vish, viajei, mestre. Quais seriam as respostas que nutrem o enunciado?

Alien supremo- Jedi

- Mensagens : 438
Data de inscrição : 20/08/2022
Idade : 22
Localização : Rio de Janeiro
 Re: Função Logaritmica
Re: Função Logaritmica
Prezados,
Para que a equação dada admita somente duas raízes reais, para todo x real, deve existir algum parâmetro real positivo t de modo que isso seja verdadeiro, por hipótese.
[latex] \underset{Hip\acute{o}tese}{\underbrace{\exists t\in \mathbb{R}_{+}^{*},\forall x \in \mathbb{R},\, \overset{(I)}{\overbrace{4^{x}-(\ln t\, +3)2^{x}-\ln t=0}} \Leftrightarrow x=x_{1}\, \, \, \vee \, \, \, x=x_{2}}}[/latex]
Como a expressão é um tanto quanto pesada de manipularmos, vamos considerar uma substituição dum y real positivo tal que ele é igual a 2x .
[latex] y=2^{x}\wedge(I)\Leftrightarrow y^{2}-(\ln t +3)y-\ln t=0, \forall y \in \mathbb{R}_{+}^{*}[/latex]
Observemos que se y é um real positivo, então as raízes dessa função do 2° que construímos devem ser necessariamente reais positivos. Por isso, a soma e o produto das raízes devem ser necessariamente positivas; soma-se a estas condições que apenas teremos as duas raízes reais positivas e diferentes se, e somente se, o discriminante for positivo. Nesse sentido, é condição necessária e suficiente à nossa hipótese que os valores do parâmetro t satisfaçam a estas 3 condições.
[latex]y^{2}-(\ln t +3)y-\ln t=0, \forall y \in \mathbb{R}_{+}^{*}\Leftrightarrow \left\{\begin{matrix} x_{1}x_{2}> 0 \, (II)\\ x_{1}+x_{2}> 0\, (III)\\ x_{1}\neq x_{2}\Leftrightarrow \Delta > 0\, (IV) \end{matrix}\right.[/latex]
Nesse ponto basta resolvermos as inequações logarítmicas, considerando a condição de existência deles satisfeitas por nossas premissas.
[latex](II): \ln t< 0\Leftrightarrow t< 1\\\\\\(III): \ln t +3> 0\Leftrightarrow t> e^{-3}\\\\\\(IV): (\ln t +3 )^2+4 \ln t > 0\Leftrightarrow t< e^{-9}\, \, \, \vee \, \, \, t> e^{-1}\\\\\\(II)\cap (III)\cap (IV)=(e^{-1},1)[/latex]
Logo, a interseção desses 3 intervalos é a solução da nossa questão.
Espero que isso tenha sanado as dúvidas dos senhores. Aguardo pelo feedback.
Para que a equação dada admita somente duas raízes reais, para todo x real, deve existir algum parâmetro real positivo t de modo que isso seja verdadeiro, por hipótese.
[latex] \underset{Hip\acute{o}tese}{\underbrace{\exists t\in \mathbb{R}_{+}^{*},\forall x \in \mathbb{R},\, \overset{(I)}{\overbrace{4^{x}-(\ln t\, +3)2^{x}-\ln t=0}} \Leftrightarrow x=x_{1}\, \, \, \vee \, \, \, x=x_{2}}}[/latex]
Como a expressão é um tanto quanto pesada de manipularmos, vamos considerar uma substituição dum y real positivo tal que ele é igual a 2x .
[latex] y=2^{x}\wedge(I)\Leftrightarrow y^{2}-(\ln t +3)y-\ln t=0, \forall y \in \mathbb{R}_{+}^{*}[/latex]
Observemos que se y é um real positivo, então as raízes dessa função do 2° que construímos devem ser necessariamente reais positivos. Por isso, a soma e o produto das raízes devem ser necessariamente positivas; soma-se a estas condições que apenas teremos as duas raízes reais positivas e diferentes se, e somente se, o discriminante for positivo. Nesse sentido, é condição necessária e suficiente à nossa hipótese que os valores do parâmetro t satisfaçam a estas 3 condições.
[latex]y^{2}-(\ln t +3)y-\ln t=0, \forall y \in \mathbb{R}_{+}^{*}\Leftrightarrow \left\{\begin{matrix} x_{1}x_{2}> 0 \, (II)\\ x_{1}+x_{2}> 0\, (III)\\ x_{1}\neq x_{2}\Leftrightarrow \Delta > 0\, (IV) \end{matrix}\right.[/latex]
Nesse ponto basta resolvermos as inequações logarítmicas, considerando a condição de existência deles satisfeitas por nossas premissas.
[latex](II): \ln t< 0\Leftrightarrow t< 1\\\\\\(III): \ln t +3> 0\Leftrightarrow t> e^{-3}\\\\\\(IV): (\ln t +3 )^2+4 \ln t > 0\Leftrightarrow t< e^{-9}\, \, \, \vee \, \, \, t> e^{-1}\\\\\\(II)\cap (III)\cap (IV)=(e^{-1},1)[/latex]
Logo, a interseção desses 3 intervalos é a solução da nossa questão.
Espero que isso tenha sanado as dúvidas dos senhores. Aguardo pelo feedback.

Lucas_DN684- Fera

- Mensagens : 100
Data de inscrição : 26/07/2022
Alien supremo gosta desta mensagem
 Gabarito errado
Gabarito errado
o gabarito ficou errado, tentei arrumar mas não consegui, peço perdão a todos
Gabarito: 0< t < e^{-9} ou t > e-3
Escrever pq com sinais não está dando:
"t está entre 0 e e-9 ou t é maior que e-3 "
*está dando problema na hora de digitar*
Gabarito: 0< t < e^{-9} ou t > e-3
Escrever pq com sinais não está dando:
"t está entre 0 e e-9 ou t é maior que e-3 "
*está dando problema na hora de digitar*
Última edição por vinimasa72 em Qui 03 Ago 2023, 19:53, editado 2 vez(es) (Motivo da edição : por algum motivo, o site ta comendo letras)
vinimasa72- Padawan

- Mensagens : 52
Data de inscrição : 20/03/2023
Idade : 19
Localização : Jundiai SP
vinimasa72- Padawan

- Mensagens : 52
Data de inscrição : 20/03/2023
Idade : 19
Localização : Jundiai SP
vinimasa72- Padawan

- Mensagens : 52
Data de inscrição : 20/03/2023
Idade : 19
Localização : Jundiai SP
 Re: Função Logaritmica
Re: Função Logaritmica
@vinimasa72,
Quando for assim, tenta digitar equações em LaTeX (Só cliclar em Pré-visualizar) ou usando os botões que aparecem nessa caixa onde você digita pra colocar expoentes etc.
Sobre o gabarito fornecido, vejo que ele diz respeito somente à condição do discriminante positivo e acaba não considerando o fato das raízes serem reais positivos, concorda?
Nesse sentido, acredito que a resolução do seu material provavelmente não está exatamente errada, mas sim incompleta porque não atende todas as condições levantadas neste tópico.
Quando for assim, tenta digitar equações em LaTeX (Só cliclar em Pré-visualizar) ou usando os botões que aparecem nessa caixa onde você digita pra colocar expoentes etc.
Sobre o gabarito fornecido, vejo que ele diz respeito somente à condição do discriminante positivo e acaba não considerando o fato das raízes serem reais positivos, concorda?
Nesse sentido, acredito que a resolução do seu material provavelmente não está exatamente errada, mas sim incompleta porque não atende todas as condições levantadas neste tópico.

Lucas_DN684- Fera

- Mensagens : 100
Data de inscrição : 26/07/2022
 Re: Função Logaritmica
Re: Função Logaritmica
____________________________________________
Charlotte de Witte - Universal Nation

Giovana Martins- Grande Mestre

- Mensagens : 8538
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo
Página 1 de 2 • 1, 2 
 Tópicos semelhantes
Tópicos semelhantes» Matemática: função exponencial e função logarítmica
» Função logaritmica e função exponencial (teórica).
» Função logarítmica
» Função Logarítmica
» Função logarítmica[2]
» Função logaritmica e função exponencial (teórica).
» Função logarítmica
» Função Logarítmica
» Função logarítmica[2]
PiR2 :: Matemática :: Álgebra
Página 1 de 2
Permissões neste sub-fórum
Não podes responder a tópicos