Cálculo de Área (UE-PI)
5 participantes
Página 1 de 1
Renato479- Iniciante
- Mensagens : 15
Data de inscrição : 27/02/2020
 Re: Cálculo de Área (UE-PI)
Re: Cálculo de Área (UE-PI)
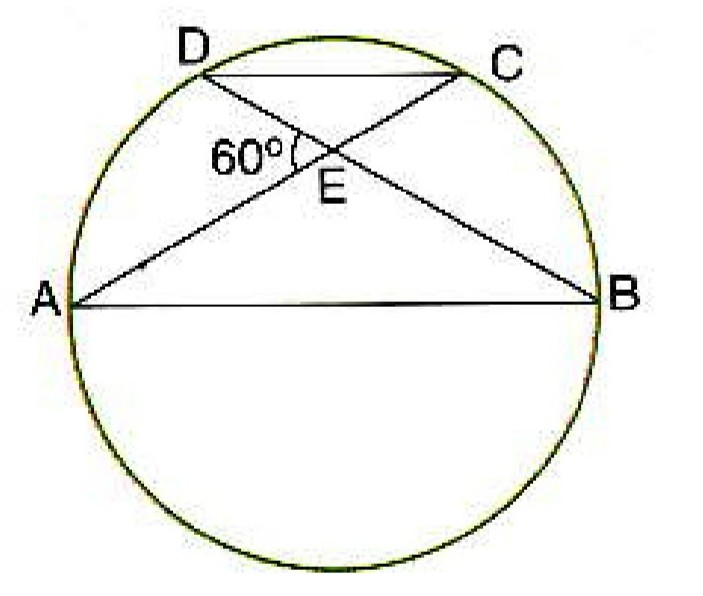
Como AB e CD são paralelas, então BÊC = AÊD = 60º e AÊB = CÊD = 180º - AÊD = 120º.
Consequentemente, por simetria da figura, tem-se que:
Consequentemente, por simetria da figura, tem-se que:
- AE = BE
- CE = DE
- BÂE = A^BE = D^CE = C^DE = (180º - AÊB)/2 = 30º
Como a área do triângulo ABE é igual a 24, então:
(1/2)*AE*BE*sen(AÊB) = 24 → (1/2)*AE²*sen(120º) = 24 → AE² = 96/√3 = 32√3 → AE = √(32√3)
Pela lei dos senos no triângulo ABE, tem-se que:
sen(AÊB)/AB = sen(A^BE)/AE → sen(120º)/AB = sen(30º)/√(32√3) → AB = √(96√3)
O ângulo A^CB é um ângulo inscrito da circunferência, e portanto é igual a metade do arco que ele estabelece na circunferência. Assim, A^CB = 180º/2 = 90º. Logo, A^BC = 180º - A^CB - BÂE = 60º.
Pela lei dos senos no triângulo ABC, tem-se que:
sen(A^CB)/AB = sen(A^BC)/(AE + CE) → sen(90º)/√(96√3) = sen(60º)/(√(32√3) + CE) → CE = 2√(2√3)
sen(A^CB)/AB = sen(A^BC)/(AE + CE) → sen(90º)/√(96√3) = sen(60º)/(√(32√3) + CE) → CE = 2√(2√3)
Logo, a área do triângulo CDE é:
Área(CDE) = (1/2)*CE*DE*sen(CÊD) = (1/2)*CE²*sen(120º) = (1/2)*4(2√3)*√3/2 = 6
Provavelmente exista uma solução mais curta usando mais as proporções da figura.

mauk03- Fera

- Mensagens : 831
Data de inscrição : 14/04/2012
Idade : 31
Localização : TB - Paraná - Br
 Re: Cálculo de Área (UE-PI)
Re: Cálculo de Área (UE-PI)
Muito obrigado pela resoluçãomauk03 escreveu:Como AB e CD são paralelas, então BÊC = AÊD = 60º e AÊB = CÊD = 180º - AÊD = 120º.
Consequentemente, por simetria da figura, tem-se que:
- AE = BE
- CE = DE
- BÂE = A^BE = D^CE = C^DE = (180º - AÊB)/2 = 30º
Como a área do triângulo ABE é igual a 24, então:(1/2)*AE*BE*sen(AÊB) = 24 → (1/2)*AE²*sen(120º) = 24 → AE² = 96/√3 = 32√3 → AE = √(32√3)Pela lei dos senos no triângulo ABE, tem-se que:sen(AÊB)/AB = sen(A^BE)/AE → sen(120º)/AB = sen(30º)/√(32√3) → AB = √(96√3)O ângulo A^CB é um ângulo inscrito da circunferência, e portanto é igual a metade do arco que ele estabelece na circunferência. Assim, A^CB = 180º/2 = 90º. Logo, A^BC = 180º - A^CB - BÂE = 60º.Pela lei dos senos no triângulo ABC, tem-se que:
sen(A^CB)/AB = sen(A^BC)/(AE + CE) → sen(90º)/√(96√3) = sen(60º)/(√(32√3) + CE) → CE = 2√(2√3)Logo, a área do triângulo CDE é:Área(CDE) = (1/2)*CE*DE*sen(CÊD) = (1/2)*CE²*sen(120º) = (1/2)*4(2√3)*√3/2 = 6Provavelmente exista uma solução mais curta usando mais as proporções da figura.
Renato479- Iniciante
- Mensagens : 15
Data de inscrição : 27/02/2020

Medeiros- Grupo
Velhos amigos do Fórum
- Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
 Re: Cálculo de Área (UE-PI)
Re: Cálculo de Área (UE-PI)
Eai Medeiros! Poderia me esclarecer aqui aquela parte em que você diz que CD = AB/2 ?
Eu não consegui ver ainda como que ele vale metade de AB.
Eu não consegui ver ainda como que ele vale metade de AB.
JMão- Jedi

- Mensagens : 305
Data de inscrição : 22/03/2017
Idade : 23
Localização : Vitória , Espírito Santo , Brasil
 Re: Cálculo de Área (UE-PI)
Re: Cálculo de Área (UE-PI)
AÔD = DÔC = CÔB = 60º
AD = DC = CD = lado do hexágono inscrito = R
AB = 2.R
AD = DC = CD = lado do hexágono inscrito = R
AB = 2.R

Elcioschin- Grande Mestre

- Mensagens : 73164
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
 Re: Cálculo de Área (UE-PI)
Re: Cálculo de Área (UE-PI)
Fala Elcio! Caramba eu não tinha pensado nisso kk muito obrigado
JMão- Jedi

- Mensagens : 305
Data de inscrição : 22/03/2017
Idade : 23
Localização : Vitória , Espírito Santo , Brasil
 Tópicos semelhantes
Tópicos semelhantes» Cálculo Integral - Problema envolvendo cálculo de área
» Cálculo de área
» Calculo de Area
» Cálculo de Área
» Cálculo de área
» Cálculo de área
» Calculo de Area
» Cálculo de Área
» Cálculo de área
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos