Raio da circunferência

por NMS50 Qua 2 Out - 10:04

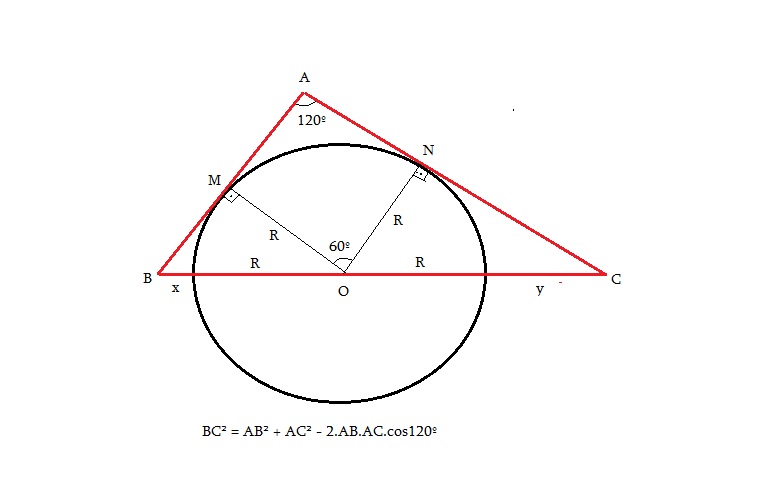
Num triângulo ABC, AB = 5 cm, AC = 8 cm e BÂC = 120°. Calcule o raio da circunferência que tem centro sobre o lado BC e é tangente aos outros lados do triângulo.
Gabarito: 20√3/13 cm.

por **Elcioschin** Qua 2 Out - 11:26

Para ajudar (não está em escala):

por **Medeiros** Qui 3 Out - 4:56

mais um pouco de ajuda (é muita conta) ...

Observe que o triângulo OMN é equilátero. Consequentemente o triângulo AMN é isósceles com 30° na base.
lei dos senos triâng AMN --> AM = AN = R.√3/3

BM = 5 - AM ---> BM
CN = 8 - AN ---> CN

triângulos BMO e CNO são retângulos, por Pitágoras calcule BO e CO.
BO + CO = BC
e, pela lei dos cossenos indicada pelo Élcio, calcule BC (acho que dá √129 = √3.√43).
Portanto vc tem tudo em função de R ---> calcule R.

por NMS50 Sáb 5 Out - 21:35

Obrigada!

por **Medeiros** Dom 6 Out - 13:41

NMS

não me conformei com aquele monte de conta (detesto algebrismo) e procurei uma solução mais fácil -- achei!!! e vou usar o desenho do Élcio.

Depois do cálculo de BC (conforme indicado pelo Élcio) e do cálculo de BM e CN (conforme indiquei anteriormente), vamos rotacionar o triângulo NOC em torno do ponto O até que o ponto N coincida com o ponto M. Ficamos com o triângulo BOC' que é semelhante ao triângulo BAC original. Note que C'O = CO.

Então basta calcular BC' e aplicar as semelhanças para obter BO e CO. Aí iguala BC = BO + CO. As contas ficam mais fáceis.