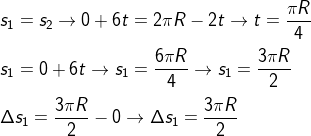movimento circular

por marcelindo3301 Qua 07 Fev 2018, 15:28

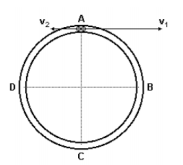
A figura uma calha circular, de raio R, completamente lisa, em posição horizontal. Dentro dela há duas bolas, 1 e 2, idênticas e em repouso no ponto A. Ambas as bolas são disparadas, simultaneamente, desse ponto: a bola 1, para a direita, com velocidade v1 =6 m/s e a bola 2, para a esquerda, com velocidade v2 = 2 m/s. As colisões entre as bolas são perfeitamente elásticas. Indique onde ocorrerá a quarta colisão entre as bolas, após o disparo delas.

A) Entre os pontos A e B
B) Exatamente no ponto A
C) Entre os pontos C e D
D) Exatamente no ponto C
E) Exatamente no ponto D

n tenho o gab

por **Giovana Martins** Qua 07 Fev 2018, 16:18

Adotemos o sentido horário como positivo. Velocidades de cada bola após a primeira colisão:

Note que as velocidades se mantiveram após a colisão. O sinal negativo indica que a bola 2, após a colisão, passou a mover-se no sentido horário. Portanto, a cada colisão está situação irá se manter.

Portanto, a esfera 1 teve de percorrer 75% da calha para encontrar a esfera 2, sendo que esta percorreu apenas 25%. Como o sistema é conservativo, uma vez que as colisões são perfeitamente elásticas, a esfera 1, em todas as sucessivas colisões, terá de percorrer 75% da calha enquanto a esfera 2 terá de percorrer 25% da calha. Logo:

Portanto, em 4 colisões, a esfera 1 percorrerá 3 voltas completas, o que indica que na quarta colisão as esferas 1 e 2 se encontraram no ponto A.

por marcelindo3301 Qua 07 Fev 2018, 16:25

Obrigado

por **Giovana Martins** Qua 07 Fev 2018, 16:28

De nada.

por **Giovana Martins** Sex 16 Fev 2018, 20:45

Um ajuste:

"O sinal negativo indica que a bola 2, após a colisão, passou a mover-se no sentido horário."

A bola 2 passa a mover-se no sentido anti-horário. Foi isso que eu quis dizer.

por nudwu92 Sáb 24 Mar 2018, 11:18

Existe outra forma de resolver?

por **Giovana Martins** Sáb 24 Mar 2018, 16:21

nudwu92, eu não consegui enxergar outra solução, mas talvez haja outra saída. Há alguma coisa que você não conseguiu entender na minha resolução?

por Raquel Valadão Ter 04 Fev 2020, 21:35

Não entendi o porquê do sinal postivo depois do movimento, se quando ha o perfeitamente elástico, uma bola vai no sentido horário e a outra no anti. Quer dizer, tem a prova disso quando se acha o -2m/s, mas não entendi o porquê disso não ser considerado no início do cálculo

E por que o So da bola 2 é 2pir e não 0 se elas saem do mesmo lugar?

por **Giovana Martins** Qua 05 Fev 2020, 00:44

Oiii, Raquel.

Honestamente, eu não me lembro o que eu pensei quando eu desenvolvi a primeira resolução principalmente quanto a convenção de sinais. Vendo a resolução hoje, ela me parece errada. Estranho que para o colega Marcelo ela fez sentido e na época que eu propus a resolução na minha mente fazia sentido também. Vou propor uma nova resolução (ignore a primeira). A propósito, eu digo que a primeira resolução está equivocada pelo seguinte motivo: em uma colisão perfeitamente elástica e unidimensional entre corpos de mesma massa ocorre a troca de velocidades entre esses corpos (se você quiser eu posto a prova desse caso). Isso não ocorreu se observarmos a primeira resolução mas deveria ter ocorrido. Agora vamos para as contas (adotando sentido horário positivo).

\[\mathrm{\vec{Q_i}=\vec{Q_f}\to mv_1-mv_2=mv_1'+mv_2'\to v_1'+v_2'=4}\]

\[\mathrm{e=\frac{|v_{Af}|}{|v_{Ap}|}=\frac{|v_2'-v_1'|}{\left |v_1-v_2 \right |}\to 1=\frac{|v_2'-v_1'|}{6+2}\to v_2'-v_1'=\pm 8}\]

\[\mathrm{\left\{\begin{matrix} v_2'-v_1'=8\\ v_1'+v_2'=4\end{matrix}\right.\to v_2'=6\ \frac{m}{s}\ \therefore \ v_1'=-2\ \frac{m}{s}}\]

\[\mathrm{\left\{\begin{matrix}v_2'-v_1'=-8\\ v_1'+v_2'=4\end{matrix}\right.\to v_2'=-2\ \frac{m}{s}\ \therefore \ v_1'=6\ \frac{m}{s}}\]

Nota¹: eu não sei para onde os corpos vão após a colisão, por isso eu mantenho o módulo.

Nota²: os resultados do segundo sistema não fazem sentido justamente pela propriedade citada anteriormente.

Do primeiro sistema concluímos que após a colisão o corpo 1 passa a mover-se no sentido anti-horário (velocidade negativa) e o corpo 2 no sentido horário (velocidade positiva). Como o sistema é conservativo essa situação vai se alternando a cada colisão. O próximo cálculo a seguir é o mesmo do anterior e equivale ao quanto que o corpo 1 percorreu para encontrar o corpo 2.

\[\mathrm{s_1=s_2\to 0+6t=2\pi R-2t\to t=\frac{\pi R}{4}}\]

\[\mathrm{s_1=0+6t\to s_1=\frac{6\pi R}{4}\to s_1=\frac{3\pi R}{2}}\]

\[\mathrm{\Delta s_1=\frac{3\pi R}{2}-0\to \Delta s_1=\frac{3\pi R}{2}}\]

Como o sistema é conservativo essa proporção será a mesma em todos os encontros alternando apenas os corpos que irão "percorrer essas proporções".

Que equivale a 75% da calha (primeira colisão a qual ocorre no ponto D). Na segunda colisão o corpo 1 percorre 25% (o corpo 2, 75%) da calha então o encontro ocorre no ponto C. De forma análoga (não se esquecendo das alternâncias de velocidades entre os corpos a cada colisão) concluímos que o quarto encontro ocorrerá no ponto A.

Algumas considerações:

"Não entendi o porquê do sinal postivo depois do movimento, se quando ha o perfeitamente elástico, uma bola vai no sentido horário e a outra no anti."

Isso nem sempre é verdade. Pegue dois corpos de mesma massa, ambos indo na mesma direção, um com velocidade de 12 m/s e outro com velocidade de 8 m/s. Para uma colisão perfeitamente elástica e unidimensional, as velocidades iram trocar mas ainda assim, após a colisão, eles irão para a mesma direção.

"E por que o So da bola 2 é 2pir e não 0 se elas saem do mesmo lugar?"

É uma questão de referencial. Os corpos estão indo em direções opostas, então um parte do zero e ou outro do 2∏R. Se ambos estivessem indo na mesma direção então ambos estariam partindo de zero.

Bom, se algo não ficar claro é só avisar.