Desenho Geométrico

Relembrando a primeira mensagem :

Boa noite, senhores!

Este problema foi proposto por um professor de minha faculdade logo no início do curso de desenho geométrico. Então, peço aos senhores para apresentar a solução geométrica para o mesmo (sem álgebra).
Dados do triângulo ABC:
\\\overhat{A}=90^\circ\\a+b=125mm\\a+c=90mm

Deve-se desenhar a solução!

Quem quiser somente mostrar o 'rascunho' da solução explicando como conseguiu chegar (obrigatoriamente por meios geométricos) digo se está correto ou não.

Posto a solução assim que alguém chegar na mesma (ou se começarem a pedir água)

Bom divertimento!

Bom dia, Medeiros!!!

O importante é que tentou montar! E eu fiquei matutando qual propriedade poderia justificar a construção geométrica. Pensei em média geométrica, em propriedade de catetos com projeção e hipotenusa... mas não tinha conseguido vislumbrar nada. Por isso perguntei sobre a diferença entre os lados (b-c) para ver o que tinha pensado!

E com certeza não foi macumba nenhuma!  hahaahah

Eu também fico envergonhado com erros, independentemente do tipo. Mas nada que tomar umas duas cervejas (ou doze) não me dê forças para dizer que errei (bêbado) e bola pra frente!

Abraços!

Bom dia, Baltuilhe!

Durante todo esse tempo não consegui pensar em mais nada e gostaria que você mostrasse a resolução. (Achou que eu tinha esquecido, né?)

Um brinde!

Medeiros, boa noite!

Hoje finalmente irei postar a solução para o problema. Andei meio afastado do fórum, mas agora voltei de vez.
Tinha a solução pronta há bastante tempo (o desenho). Só faltava postar, mesmo.
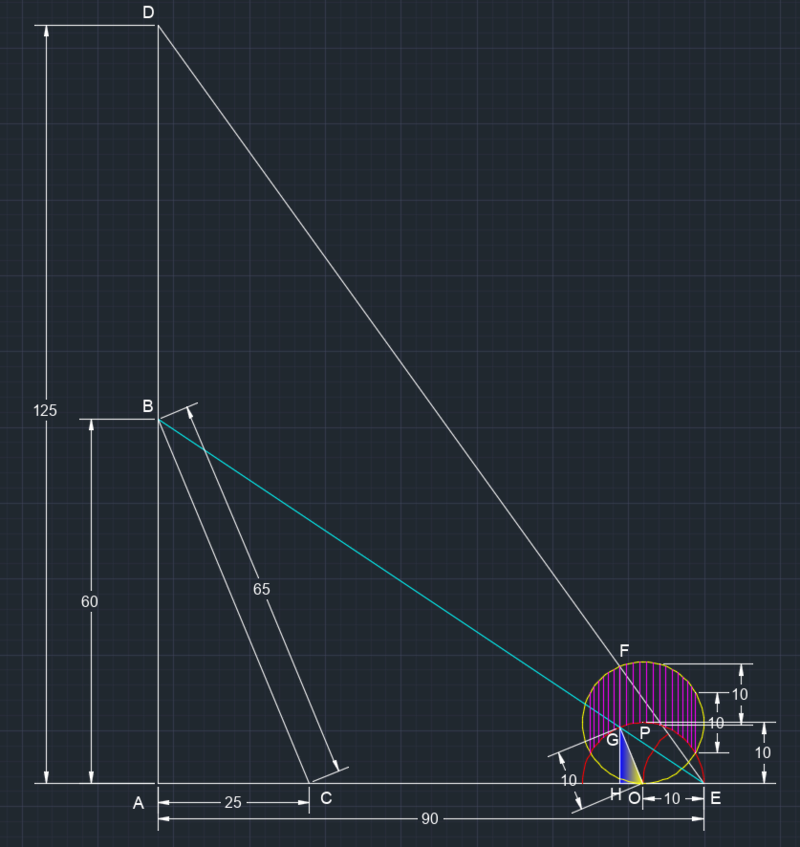
A solução é a seguinte (passos):

1) Desenhar os segmentos de tamanho a+b=125cm e a+c=90cm perpendicularmente um ao outro e 'fechar' o triângulo com catetos 125 e 90.
2) Desenhar um arco de tamanho qualquer no ponto E (desenhei de tamanho 10, mas pode ser qualquer).
3) Traçar a semi-circunferência com centro no ponto O, interseção do arco anterior, onde o arco anterior marcou o segmento AE.
4) Desenhar uma circunferência de mesmo raio (o mesmo raio qualquer que arbitrou inicialmente) na posição P (ponto da circunferência de centro em O), segmento OP é perpendicular a AE.
5) Esta circunferência encontra o segmento DE no ponto F, e o segmento GF (que é perpendicular ao AE) tem mesma medida do raio arbitrário).
6) Veja que este raio aparece em GF, OG e OE, certo? O triângulo OGH é um triângulo semelhante à resposta.
7) Por HOMOTETIA (o segmento EG é prolongado até encontrar o segmento AE no ponto B) encontramos a solução.
É isso!

Abraços!

Olá Baltuilhe
boa tarde, depois de um longo inverno (ops, ainda estamos no inverno... de 2018)!

Excelente e genial solução. Eu nunca chegaria nela. Obrigado por mostrar.

Você não descreveu mas, por óbvio, creio que seria: por B trace uma paralela a OG obtendo o ponto C na intersecção com AE.

Um grande abraço, tin-tin!

Medeiros escreveu:Olá Baltuilhe
boa tarde, depois de um longo inverno (ops, ainda estamos no inverno... de 2018)!

Excelente e genial solução. Eu nunca chegaria nela. Obrigado por mostrar.

Você não descreveu mas, por óbvio, creio que seria: por B trace uma paralela a OG obtendo o ponto C na intersecção com AE.

Um grande abraço, tin-tin!

Boa tarde!

Realmente, ficou faltando esta óbvia parte... que obviamente esqueci de escrever
Um grande abraço!!!

Rodrigo

Um grande abraço, Rodrigo.

continuo babando pela bonita solução. Mas que sacada genial fazer aquela "rodinha" (circunf.) no ponto exato e usar o raio para criar um semelhante!!!!

Então, Medeiros!

Levei bastante tempo para chegar nessa solução, meu amigo!
Foram uns 5 anos... não tentando todos os dias... mas sempre que lembrava... dava umas noites sem dormir  Mas enquanto não consegui... não sosseguei

Taí uma solução que dificilmente fugirá de minha mente!

Abraços!