CIABA

(CIABA) Um triângulo obtusângulo ABC tem 18cm de perímetro e as medidas de seus lados formam uma Progressão Aritmética crescente 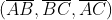. Os raios das circunferências inscrita e circunscrita a esse triângulo ABC medem, respectivamente, r e R. S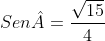e  e 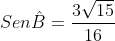 então o produto r . R em cm², é igual a?

Não sei o gabarito e nem se tem alternativa, essa é uma questão que um professor passou no ano passado em um cursinho, desculpem.

Faça um bom desenho

Sejam AB = x - r, BC = x, CA = x + r

(x - r) + x + (x + r) = 18 ----> x = 6 ---> AB = 6 - r, BC = 6, CA = 6 + r

senA = √15/4 ---> sen²A = 15/16 ---> cos²A = 1/6 ---> cosA = 1/4

senB = 3√15/16 ---> sen²B = 135/256 ---> cos²B = 121/256 ---> cosB = 11/16

A + B + C = 180º ---> A + B = 180º - C ---> sen(A + B) = sen(180º - C) --->

sen(A + B) = senC ---> senA.cosB + senB.cosA = senC --->

senC = (√15/4).(11/16) + (3.√15/16).(1/4) ---> senC = 11.√15/64 + 3.√15/64 -->

senC = 7.√15/32

Use agora ---> AB/senC = BC/senA = AC/senB = 2R ----> Raio da circunferência circunscrita

Use também a lei dos cossenos

E tente completar

Elcioschin escreveu:Faça um bom desenho

Sejam AB = x - r, BC = x, CA = x + r

(x - r) + x + (x + r) = 18 ----> x = 6 ---> AB = 6 - r, BC = 6, CA = 6 + r

senA = √15/4 ---> sen²A = 15/16 ---> cos²A = 1/6 ---> cosA = 1/4

senB = 3√15/16 ---> sen²B = 135/256 ---> cos²B = 121/256 ---> cosB = 11/16

A + B + C = 180º ---> A + B = 180º - C ---> sen(A + B) = sen(180º - C) --->

sen(A + B) = senC ---> senA.cosB + senB.cosA = senC --->

senC = (√15/4).(11/16) + (3.√15/16).(1/4) ---> senC = 11.√15/64 + 3.√15/64 -->

senC = 7.√15/32

Use agora ---> AB/senC = BC/senA = AC/senB = 2R ----> Raio da circunferência circunscrita

Use também a lei dos cossenos

E tente completar

E depois para achar r, não entendi?

Essa questão não foi digitada corretamente, o enunciado original da prova da EFOMM 2011 diz que a PA é (AB,AC,BC)

PA--> AB+BC=2AC e AB+AC+BC=18
2AC+AC=18
AC=6 cm

AC/senB=2R 
6/3V15/16=2R
32/V15=2R
R=16/V15

BC/senA=2R
BC/V15/4=32/V15
4BC=32
BC=8 cm

AB+AC+BC=18
AB+6+8=18
AB=4 cm

Área de um triângulo circunscrito em uma circunferência: S=p.r (semiperímetro.raio)
Área de um triângulo inscrito em uma circunferência: S=AB.AC.BC/4R

r=S/p  ;  R=AB.AC.BC/4S

r.R= (S/p).(AB.AC.BC/4S)
r.R=4.6.8/4.9
r.R=48/9
r.R=16/3 cm²

RodrigoA.S escreveu:Essa questão não foi digitada corretamente, o enunciado original da prova da EFOMM 2011 diz que a PA é (AB,AC,BC)

PA--> AB+BC=2AC e AB+AC+BC=18
2AC+AC=18
AC=6 cm

AC/senB=2R 
6/3V15/16=2R
32/V15=2R
R=16/V15

BC/senA=2R
BC/V15/4=32/V15
4BC=32
BC=8 cm

AB+AC+BC=18
AB+6+8=18
AB=4 cm

Área de um triângulo circunscrito em uma circunferência: S=p.r (semiperímetro.raio)
Área de um triângulo inscrito em uma circunferência: S=AB.AC.BC/4R

r=S/p  ;  R=AB.AC.BC/4S

r.R= (S/p).(AB.AC.BC/4S)
r.R=4.6.8/4.9
r.R=48/9
r.R=16/3 cm²

Muito obrigado