Geometria - Prismas

por Lukash10 Qua 29 maio 2013, 00:11

Calcule as dimensoes de um ortoedro cuja diagonal mede 13 cm, de área total 192 cm^2, e sabendo que a área da secçao por um plano por duas arestas opostas é 60 cm.

OBs: O Enunciado é esse mesmo .. Direto do Fundamentos da Matemática Elementar.

Spoiler:

por Victor Luz Sáb 13 Jan 2018, 01:14

Perdão ressuscitar o tópico mas alguém poderia fazer? Não consegui entender a frase final do enunciado.

por evandronunes Sáb 13 Jan 2018, 19:12

A área da secção que ele descreve é a da figura abaixo.

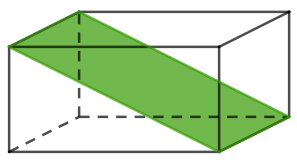
Seja x a largura, y o comprimento e z a altura desse sólido.

Temos:

2(xy+yz+xz) = 192 \ \ \Rightarrow \ \ xy+yz+xz=96 \ \ \ (1)

\sqrt{x^2+y^2+z^2}=13 \ \ \Rightarrow \ \ y^2+z^2=169-x^2

A área em destaque é dada por x. \sqrt{y^2+z^2}=60. De onde vem,

x. \sqrt{169-x^2}=60

x^4-169x^2+3600=0

Cujas as raízes positivas são x = 12 e x = 5.

Temos que

(x+y+z)^2=x^2+y^2+z^2+2(xy+yz+xz)

(x+y+z)^2=169+192

x+y+z =19 \ \ \ (2)

Substituindo x = 12 em (1) e (2), vem y +z=7 e y.z=12, onde as soluções são 3 e 4.

Substituindo x = 5 em (1) e (2), vem y +z=14 e y.z=26, onde as soluções são 7+ \sqrt{23} e 7- \sqrt{23}.

por Conteúdo patrocinado

Geometria - Prismas

Geometria - Prismas

Re: Geometria - Prismas

Re: Geometria - Prismas

Re: Geometria - Prismas

Um fórum livre e democrático.