Segmentos do Triângulo

por matheus_feb Sáb 21 Set 2024, 21:32

Relembrando a primeira mensagem :

1) Um ateliê fabrica molduras em formatos diversos. Uma dessas molduras possui formato de triângulo equilátero com 48 cm de lado. Para auxiliar no suporte da tela que vai na moldura, três varetas partem de um ponto P interno ao triângulo em direção aos lados, conforme a imagem a seguir:

Segmentos do Triângulo - Página 3 W97BsnvN4aD0QAAAABJRU5ErkJggg==

Segmentos do Triângulo - Página 3 W97BsnvN4aD0QAAAABJRU5ErkJggg==

A soma dos comprimentos das varetas, em cm, é igual a:

a) 16.
b) 12√3
c) 24
d) 24√3
e) 72

por **Matheus Tsilva** Dom 22 Set 2024, 23:24

Giovana Martins escreveu:
Matheus Tsilva escreveu:
Giovana Martins escreveu:

Ainda da construção gráfica:

\[\mathrm{BD+CE+AF=AE+CD+BF=k,com\ k\ constante}\]

não consegui visualizar esse passo aqui ainda

esse triangulo IJH criado é equilatero ?

Sim, sim. À noite eu faço mais algumas construções.

show

por **Giovana Martins** Seg 23 Set 2024, 18:14

Matheus, veja:

Primeiramente, observe que eu adicionei o ponto G na figura para facilitar as ideias geométricas abaixo.

PL // CD ∴ ∠DCE = ∠PGE = 60°

Note que o triângulo EGP é retângulo em E. Sendo ∠PGE = 60°, logo, ∠EPG = 30°.

Observe também que ∠EPM = 90°. Assim, do quadrilátero ILPM:

∠AIL + ∠ILG + ∠EPG + ∠EPM + ∠AMP = 360°

∠AIL + 90° + 30° + 90° + 90° = 360°

Logo, ∠AIL = 60°. Analogamente você descobre ∠ILH = ∠IHJ = 60°, o que confirma que o triângulo IJH é equilátero.

Agora, quanto a igualdade das somas, veja, por meio de uma imagem, o que eu o Medeiros queremos dizer:

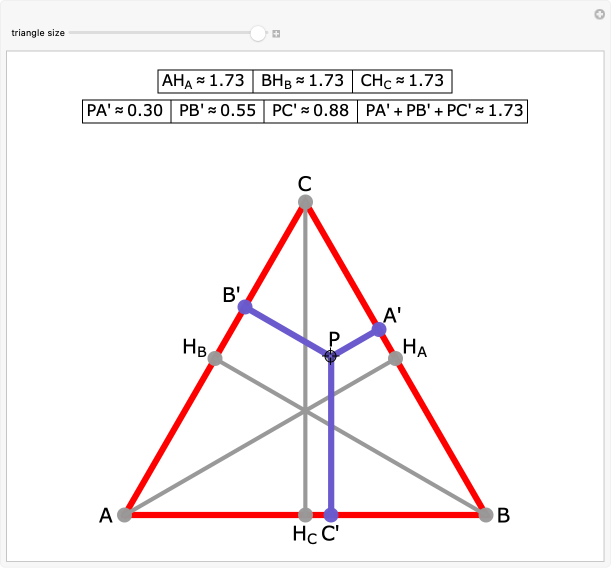
Segmentos do Triângulo - Página 3 VivianisTheorem_Snapshot-1

Veja que ao deslocar o ponto P (em roxo), os segmentos se reposicionam, embora a soma se mantém constante.

Se não tiver ficado claro, é só falar que eu tento dar um jeito de melhorar a explicação.

por **Giovana Martins** Seg 23 Set 2024, 18:15

Ah, e desculpe a demora Embarassed

.

por **Matheus Tsilva** Seg 23 Set 2024, 18:53

Giovana Martins escreveu:
Matheus, veja:

Primeiramente, observe que eu adicionei o ponto G na figura para facilitar as ideias geométricas abaixo.

PL // CD ∴ ∠DCE = ∠PGE = 60°

Note que o triângulo EGP é retângulo em E. Sendo ∠PGE = 60°, logo, ∠EPG = 30°.

Observe também que ∠EPM = 90°. Assim, do quadrilátero ILPM:

∠AIL + ∠ILG + ∠EPG + ∠EPM + ∠AMP = 360°

∠AIL + 90° + 30° + 90° + 90° = 360°

Logo, ∠AIL = 60°. Analogamente você descobre ∠ILH = ∠IHJ = 60°, o que confirma que o triângulo IJH é equilátero.

Agora, quanto a igualdade das somas, veja, por meio de uma imagem, o que eu o Medeiros queremos dizer:

Veja que ao deslocar o ponto P (em roxo), os segmentos se reposicionam, embora a soma se mantém constante.

Se não tiver ficado claro, é só falar que eu tento dar um jeito de melhorar a explicação.

perfeito
consegui visualizar

provando que o triangulo IJH é equilátero e que PM + PQ + PL = AE + CD + BF = k

PM + PQ + PL = V3.L/4 ----> l o lado do triangulo ABC e L o lado de IJH

L = l/sen60 + l/tg60 ---> L = V3.l

Pelo teorema: PM + PQ + PL = V3.L/2 ----> PM + PQ + PL = 3.l/2 = AE + CD + BF

(PD + PE + PF)/(AE + CD + BF) = (V3.l/2)/(3.l/2) = V3/3

show, obrigado

por **Giovana Martins** Seg 23 Set 2024, 19:18

Excelente, Matheus.

Os outros desafios eu posto até amanhã.

por **Matheus Tsilva** Seg 23 Set 2024, 19:24

Giovana Martins escreveu:
Excelente, Matheus.

Os outros desafios eu posto até amanhã.

tem mais desafio ainda, kkkk
visshhh

por **Giovana Martins** Seg 23 Set 2024, 19:26

Tem estes dois. Esse teorema tem muita coisa sobre ele, mas muito pouco divulgado no nosso idioma. Infelizmente.

Mostre que:

\[\mathrm{\frac{1}{PD}+\frac{1}{PE}+\frac{1}{PF}\geq \frac{6\sqrt{3}}{L}}\]

\[\mathrm{\frac{1}{PD+PE}+\frac{1}{PE+PF}+\frac{1}{PD+PF}\geq \frac{3\sqrt{3}}{L}}\]

por matheus_feb Seg 23 Set 2024, 20:28

Giovana Martins escreveu:
Tem estes dois. Esse teorema tem muita coisa sobre ele, mas muito pouco divulgado no nosso idioma. Infelizmente.

Mostre que:

\[\mathrm{\frac{1}{PD}+\frac{1}{PE}+\frac{1}{PF}\geq \frac{6\sqrt{3}}{L}}\]

\[\mathrm{\frac{1}{PD+PE}+\frac{1}{PE+PF}+\frac{1}{PD+PF}\geq \frac{3\sqrt{3}}{L}}\]

Boa noite! Fiquei muito surpreso que essa questão, que retirei de um vestibular para o ENEM, gerou tanta repercussão entre vocês! haha.

Mas isso é muito legal. Ver que uma simples questão pode se destrinchar em problemas ainda mais difíceis, e acabam ajudando muito na compreensão profunda da própria Matemática! Razz

por **Matheus Tsilva** Seg 23 Set 2024, 21:33

Giovana Martins escreveu:
Tem estes dois. Esse teorema tem muita coisa sobre ele, mas muito pouco divulgado no nosso idioma. Infelizmente.

Mostre que:

\[\mathrm{\frac{1}{PD}+\frac{1}{PE}+\frac{1}{PF}\geq \frac{6\sqrt{3}}{L}}\]

\[\mathrm{\frac{1}{PD+PE}+\frac{1}{PE+PF}+\frac{1}{PD+PF}\geq \frac{3\sqrt{3}}{L}}\]

eita kkkk
tomaaaa

e onde vc viu essas coisas ai ?

por **Giovana Martins** Seg 23 Set 2024, 22:07

Matheus Tsilva escreveu:
Giovana Martins escreveu:
Tem estes dois. Esse teorema tem muita coisa sobre ele, mas muito pouco divulgado no nosso idioma. Infelizmente.

Mostre que:

\[\mathrm{\frac{1}{PD}+\frac{1}{PE}+\frac{1}{PF}\geq \frac{6\sqrt{3}}{L}}\]

\[\mathrm{\frac{1}{PD+PE}+\frac{1}{PE+PF}+\frac{1}{PD+PF}\geq \frac{3\sqrt{3}}{L}}\]
eita kkkk
tomaaaa

e onde vc viu essas coisas ai ?

Então, o exercício da razão lá, eu lembro de ter visto em algum livro peruano que, infelizmente, eu não vou me recordar qual é.

Essas desigualdades aí você as encontra em livros de olimpíadas. Por exemplo, Titu Andreescu. Caso tenha interesse, procure por Inequalities Titu Andreescu. São alguns volumes. Em algum deles você encontra alguns tópicos sobre o Teorema de Viviani.