Questão de cinemática - MRU intervalos de tempo

por lucyln01 Sáb 30 Mar 2024, 17:10

Considere dois navios de guerra, uma Fragata e uma Corveta navegando paralelamente em sentidos opostos em um trecho retilíneo.

Sabe-se que a Corveta tem 80 metros e se move em um MRU com velocidade de 20 m/s e a Fragata possui 130 metros de comprimento e se move em um MRU com velocidade de 10 m/s. considerando que as águas estão paradas, então o intervalo de tempo que dura o cruzamento dos navios, em segundos, é de:

Pessoal, no gabarito está dando: Sc = Sb
0 + 20t = (80 + 130) - 10t
30t = 210
t= 7seg

Eu não entendi, de onde ele tirou esse 0 + 20t = (80 + 130) - 10t
De onde ele tirou isso?? O que é essa formula?

por Graphiel404 Sáb 30 Mar 2024, 18:19

Olá, Lucy! Como vai?

O livro refere-se à fórmula S = S₀+Vt, onde "S" é o espaço em algum instante "t".

A resolução do livro baseia-se na perspectiva de que os navios são pontos materiais, ou seja, seus tamanhos são desprezíveis, e que o navio Fragata precisa "alcançar" o navio Corveta.

É meio confuso, por isso acredito que seja importante visualizar:

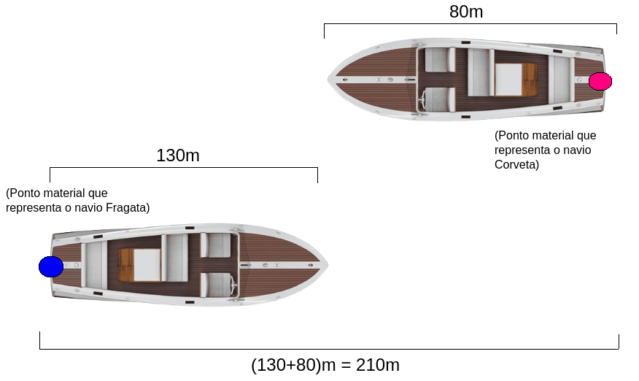
Questão de cinemática - MRU intervalos de tempo Screen13

Antes de mais nada, eu sei, a imagem está linda.

Continuando, a resolução do livro imagina os navios Fragata e Corveta como pontos materiais extremamente pequenos localizados na extremidade traseira dos navios, como se o ponto azul e o ponto rosa precisassem percorrer o comprimento dos dois barcos para se encontrarem. Por isso o livro utiliza a função horária dos espaços, pois ele quer saber o ponto onde as duas partículas se encontram.
Assumimos que o espaço inicial S₀ do ponto azul é 0 e que o ponto inicial do ponto rosa é (130+80)m = 210m, daí que surge "20t + 0 = -10t + 210".

Entretanto eu fiz de outra forma, utilizando velocidade relativa:

1) Como os navios estão navegando em movimento retilínio uniforme (ou seja, em linha reta com velocidade constante) e sentidos opostos, eu imaginei que na perspectiva do navio Corveta, o navio Fragata estaria parado, daí o navio Corveta, nessa perspectiva, teria velocidade igual a soma da velocidade dele e da velocidade do Fragata. Em outras palavras, a velocidade do navio Corveta em relação ao navio Fragata é:

[latex]|V'_{c}| = |V_{c}|+|V_{f}| = |20m/s|+|10m/s| =30m/s[/latex]

Obs.: |V'_c| é o módulo de V'_c (observe o tracinho ' ao lado do V_c, ele indica que V'_cé diferente de V_c), que equivale à velocidade relativa do Corveta em relação ao Fragata.

2) Como a velocidade do Corveta em relação ao Fragata é constante e igual à 30m/s e ele precisa percorrer o seu comprimento mais o comprimento do navio Fragata, então:

[latex]30m/s=\frac{130m+80m}{\Delta t} \Rightarrow \Delta t=7s[/latex]

3) Caso não tenha entendido porque a velocidade de C em relação a F é igual a |V_c|+ |V_f|: Imagine que você esteja em um navio no meio do mar navegando em linha reta, se você visse outro barco paralelo ao seu indo ao sentido oposto da sua trajetória, como na imagem acima, se você não for atenta ficará com dúvidas se o outro navio está parado e você está em movimento, ou se o outro navio está em movimento e você parado, ou ainda se os dois estão em movimento. Isso acontece porque em alto-mar não teríamos muitos objetos na paisagem para utilizar como referência, essa é a sacada da velocidade relativa entre dois corpos: Para você o outro móvel está parado e você está em movimento, para o outro móvel você está parado e ele em movimento. Por isso, para o instante do ponto de encontro ser o mesmo somamos o módulo das velocidades. Caso estivessem deslocando-se no mesmo sentido então subtrairíamos (|V_a| - |V_b|) para manter o instante do ponto de encontro o mesmo.

por lucyln01 Sáb 30 Mar 2024, 19:49

Neste "20t + 0 = -10t + 210".
Esse -10 na velocidade seria como se estivesse com um movimento negativo né? voltando?

Consegui entender a sacada da velocidade relativa, nunca tinha entendido, obrigada por isso