Binômio de Newton

por Amanda0144 Qua 20 Jul 2011, 21:32

A solução da equação a seguir é um número inteiro múltiplo de:

$\tiny \frac{\binom{n+1}{4}}$
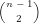
$\tiny \binom{n-1}{2}$

= 7/2

a) 11 b)9 c)7 d)5 e)3

por **Elcioschin** Qui 21 Jul 2011, 10:07

C(n+1, 4) = (n + 1)!/4!(n + 1 - 4)! = (n + 1)*n*(n - 1)!/24*(n - 3)!

C(n-1, 2) = (n - 1)!/2!*(n - 1 - 2)! = (n - 1)!/2*(n - 3)!

C(n+1, 4)/C(n-1, 2) = 7/2

[(n + 1)*n*(n - 1)!/24*(n - 3)!]/ (n - 1)!/2*(n - 3)! = 7/2

(n + 1)*n/12 = 7/2

n² + 2n - 42 = 0 ---> Raíz positiva ----> n = 6 ----> Alternativa E

Binômio de Newton

Binômio de Newton

Re: Binômio de Newton

Um fórum livre e democrático.