Triângulo Qualquer
3 participantes
Página 1 de 1
Triângulo Qualquer
por ana_karenina Qua 06 Jun 2018, 22:06
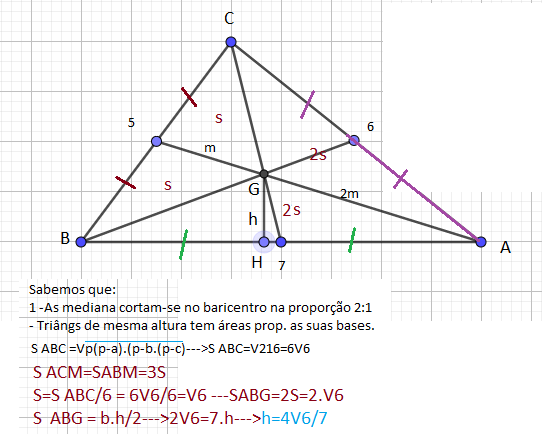
Os lados de um triângulo são: AB= 6 cm, AC= 7 cm e BC= 5 cm. Calcular a distância do ponto de concurso das medianas ao lado AC
gabarito: 4√6/7 cm
Obrigada desde já!
gabarito: 4√6/7 cm
Obrigada desde já!
Última edição por ana_karenina em Qui 07 Jun 2018, 17:55, editado 1 vez(es)
ana_karenina- Iniciante
- Mensagens : 14
Data de inscrição : 06/06/2018
Idade : 27
Localização : Natal, Rio Grande do Norte, Brasil
Re: Triângulo Qualquer
por Diego A Qui 07 Jun 2018, 16:14
por geo analítica
A(0,0), B(x,y), C(7,0)
Cordenadas do baricentro
xb = (0 + x + 7)/3
yb = (0 + y + 0)/3
Descobrindo yb saberemos a distância do segmento AC
Descobrindo as cordenadas de B
6^2 = y^2 + x^2
5^2 = y^2 + (7-x)^2
y = √(3456/196)
Assim,
yb = (0 + y + 0)/3
= (0 + √(3456/196) + 0)/3
= √(3456/196)/3
= 4√6/7
A(0,0), B(x,y), C(7,0)
Cordenadas do baricentro
xb = (0 + x + 7)/3
yb = (0 + y + 0)/3
Descobrindo yb saberemos a distância do segmento AC
Descobrindo as cordenadas de B
6^2 = y^2 + x^2
5^2 = y^2 + (7-x)^2
y = √(3456/196)
Assim,
yb = (0 + y + 0)/3
= (0 + √(3456/196) + 0)/3
= √(3456/196)/3
= 4√6/7
____________________________________________
*Se sua dúvida foi solucionada, marque o tópico como resolvido e agradeça quem ajudou.
*Não crie novo tópico para questão existente, comente junto dessa. (V)
*O enunciado da questão deve ser digitado. Também não são permitidos links externos para o enunciado e/ou para a resolução. (IX e X)
"A liberdade, se é que significa alguma coisa, significa o nosso direito de dizer às pessoas o que não querem ouvir."
Discussões no PiR2: Sexualidade - Foucault // Vias filosóficas
Diego A- Monitor
- Mensagens : 1398
Data de inscrição : 20/04/2016
Idade : 28
Localização : Cascavel - PR
Re: Triângulo Qualquer
por ana_karenina Qui 07 Jun 2018, 16:33
Oi, Diogo, tudo bem?
Primeiramente, agradeço por sua disposição em ajudar e resolução.
Segundamente, vou tentar entender a resolução, ainda não vi GA esse ano e essa questão está no meu capítulo de geometria plana.
Sei que as coisas na matemática não são separadas e tudo funciona em conjunto, eu até gosto bastante de GA, mas nem pensei em fazer por esse caminho. Vou tentar entender sozinha.
De qualquer forma, muito obrigada. É sempre bom descobrir novos caminhos.
Bom resto de semana para você.
Primeiramente, agradeço por sua disposição em ajudar e resolução.
Segundamente, vou tentar entender a resolução, ainda não vi GA esse ano e essa questão está no meu capítulo de geometria plana.
Sei que as coisas na matemática não são separadas e tudo funciona em conjunto, eu até gosto bastante de GA, mas nem pensei em fazer por esse caminho. Vou tentar entender sozinha.
De qualquer forma, muito obrigada. É sempre bom descobrir novos caminhos.
Bom resto de semana para você.
ana_karenina- Iniciante
- Mensagens : 14
Data de inscrição : 06/06/2018
Idade : 27
Localização : Natal, Rio Grande do Norte, Brasil
Re: Triângulo Qualquer
por Diego A Qui 07 Jun 2018, 16:52
de nada!
Se encontrar um modo de fazer por geo plana, eu posto pra vc
Igualmente..
Se encontrar um modo de fazer por geo plana, eu posto pra vc
Igualmente..
____________________________________________
*Se sua dúvida foi solucionada, marque o tópico como resolvido e agradeça quem ajudou.
*Não crie novo tópico para questão existente, comente junto dessa. (V)
*O enunciado da questão deve ser digitado. Também não são permitidos links externos para o enunciado e/ou para a resolução. (IX e X)
"A liberdade, se é que significa alguma coisa, significa o nosso direito de dizer às pessoas o que não querem ouvir."
Discussões no PiR2: Sexualidade - Foucault // Vias filosóficas
Diego A- Monitor
- Mensagens : 1398
Data de inscrição : 20/04/2016
Idade : 28
Localização : Cascavel - PR
ana_karenina- Iniciante
- Mensagens : 14
Data de inscrição : 06/06/2018
Idade : 27
Localização : Natal, Rio Grande do Norte, Brasil
raimundo pereira- Grupo
Velhos amigos do Fórum
- Mensagens : 6114
Data de inscrição : 13/06/2012
Idade : 83
Localização : Rio de Janeiro
Re: Triângulo Qualquer
por ana_karenina Qui 07 Jun 2018, 23:21
Diogo e Raimundo, vocês estão me ajudando muito!
Posso afirmar que o baricentro dividi o triângulo em 3 triângulos de áreas iguais cada?
Posso afirmar que o baricentro dividi o triângulo em 3 triângulos de áreas iguais cada?
ana_karenina- Iniciante
- Mensagens : 14
Data de inscrição : 06/06/2018
Idade : 27
Localização : Natal, Rio Grande do Norte, Brasil
raimundo pereira- Grupo
Velhos amigos do Fórum - Mensagens : 6114
Data de inscrição : 13/06/2012
Idade : 83
Localização : Rio de Janeiro
Tópicos semelhantes» Triângulo Qualquer
» Triângulo Qualquer
» Triângulo qualquer.
» Triângulo qualquer
» Triângulo Qualquer
» Triângulo Qualquer
» Triângulo qualquer.
» Triângulo qualquer
» Triângulo Qualquer
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
