O quadrilátero da figura

O quadrilátero da figura está inscrito em uma circunferência de raio 1. A diagonal desenhada é um diâmetro dessa circunferência.



Sendo x e y as medidas dos ângulos indicados na figura, a área da região cinza, em função de xe y, é:


a) 

b) 

c) 

d)

e)

Sejam A o vértice superior, B a extremidade direita do diâmetro, C o vértice inferior e D a extremidade esquerda do diâmetro. Seja O o centro do diâmetro BD

arco AD = 2.x = AÔD ----> arco AB = 180º - 2.x = AÔB ---> sen(180º- 2.x) = sen(2.x)
arco BC = 2.y = BÔC ----> arco CD = 180º - 2.y = CÔD ---> sen(180º - 2.y) =m sen(2.y)

OA = OB = OC = OD = 1

Área do ∆ OAD ---> S(OAD) = OA.OD.(senAÔD)/2 ---> S(OAD) = sen(2.x)/2
Área do ∆ OAB ---> S(OAB) = OA.OB.(senAÔB)/2 ---> S(OAB) = sen(2.x)/2

Área do ∆ OBC ---> S(OBC) = OB.OC.(senBÔC)/2 ---> S(OBC) = sen(2.y)/2
Área do ∆ OCD ---> S(OCD) = OC.OD.(senCÔD)/2 ---> S(OCD) = sen(2.x)/2

S = Sc - S(OAD) - S(OAB) - S(OBC) - S(OCD)

S = pi.1² - sen(2.x)/2 - sen(2.x)/2 - sen(2.y)/2 - sen(2.y)/2

S = pi - sen(2.x) - sen(2.y)

Elcioschin escreveu:Sejam A o vértice superior, B a extremidade direita do diâmetro, C o vértice inferior e D a extremidade esquerda do diâmetro. Seja O o centro do diâmetro BD

arco AD = 2.x = AÔD ----> arco AB = 180º - 2.x = AÔB ---> sen(180º- 2.x) = sen(2.x)
arco BC = 2.y = BÔC ----> arco CD = 180º - 2.y = CÔD ---> sen(180º - 2.y) =m sen(2.y)

OA = OB = OC = OD = 1

Área do ∆ OAD ---> S(OAD) = OA.OD.(senAÔD)/2 ---> S(OAD) = sen(2.x)/2
Área do ∆ OAB ---> S(OAB) = OA.OB.(senAÔB)/2 ---> S(OAB) = sen(2.x)/2

Área do ∆ OBC ---> S(OBC) = OB.OC.(senBÔC)/2 ---> S(OBC) = sen(2.y)/2
Área do ∆ OCD ---> S(OCD) = OC.OD.(senCÔD)/2 ---> S(OCD) = sen(2.x)/2

S = Sc - S(OAD) - S(OAB) - S(OBC) - S(OCD)

S = pi.1² - sen(2.x)/2 - sen(2.x)/2 - sen(2.y)/2 - sen(2.y)/2

S = pi - sen(2.x) - sen(2.y)

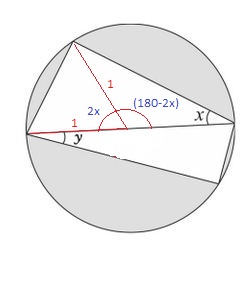
Elcio, fiz pelo Teorema das Áreas e área do triângulo do ângulo x ficou 1/2.1.1.sen(2x)+1/2.1.1.sen(180-2x) e o mesmo para o triângulo do ângulo y, mas não consegui desenvolver para chegar em sen(2x) e sen (2y). Tem como desenvolver isso e chegar a uma resposta correta ou está errado? Aqui está uma imagem do meu raciocínio para utilizar o teorema das áreas
 

fefe_legioXIII escreveu:

Elcioschin escreveu:Sejam A o vértice superior, B a extremidade direita do diâmetro, C o vértice inferior e D a extremidade esquerda do diâmetro. Seja O o centro do diâmetro BD

arco AD = 2.x = AÔD ----> arco AB = 180º - 2.x = AÔB ---> sen(180º- 2.x) = sen(2.x)
arco BC = 2.y = BÔC ----> arco CD = 180º - 2.y = CÔD ---> sen(180º - 2.y) =m sen(2.y)

OA = OB = OC = OD = 1

Área do ∆ OAD ---> S(OAD) = OA.OD.(senAÔD)/2 ---> S(OAD) = sen(2.x)/2
Área do ∆ OAB ---> S(OAB) = OA.OB.(senAÔB)/2 ---> S(OAB) = sen(2.x)/2

Área do ∆ OBC ---> S(OBC) = OB.OC.(senBÔC)/2 ---> S(OBC) = sen(2.y)/2
Área do ∆ OCD ---> S(OCD) = OC.OD.(senCÔD)/2 ---> S(OCD) = sen(2.x)/2

S = Sc - S(OAD) - S(OAB) - S(OBC) - S(OCD)

S = pi.1² - sen(2.x)/2 - sen(2.x)/2 - sen(2.y)/2 - sen(2.y)/2

S = pi - sen(2.x) - sen(2.y)

Elcio, fiz pelo Teorema das Áreas e área do triângulo do ângulo x ficou 1/2.1.1.sen(2x)+1/2.1.1.sen(180-2x) e o mesmo para o triângulo do ângulo y, mas não consegui desenvolver para chegar em sen(2x) e sen (2y). Tem como desenvolver isso e chegar a uma resposta correta ou está errado? Aqui está uma imagem do meu raciocínio para utilizar o teorema das áreas
 

Basta mostrar que

sen(180-2x) = sen(180)cos(2x)-sen(2x)cos180=0-(-sen(2x) =sen(2x)