Derivadas
2 participantes
Página 1 de 1
 Derivadas
Derivadas
Considere a figura abaixo. Suponha que os comprimentos dos segmentos AB e OB sejam, respectivamente, 5cm e 3cm. Suponha ainda, que θ esteja variando a uma taxa constante de (1/2)rad/s. Determine a velocidade de A, quando θ=(π/2)rad.
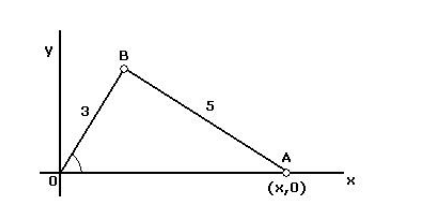
Resposta: (-3/2)cm/s. Essa questão é do livro do prof. Guidorizzi 5ª edição pagina 203
______________________________________________________________________________________________________
Galera, fiz da seguinte forma:
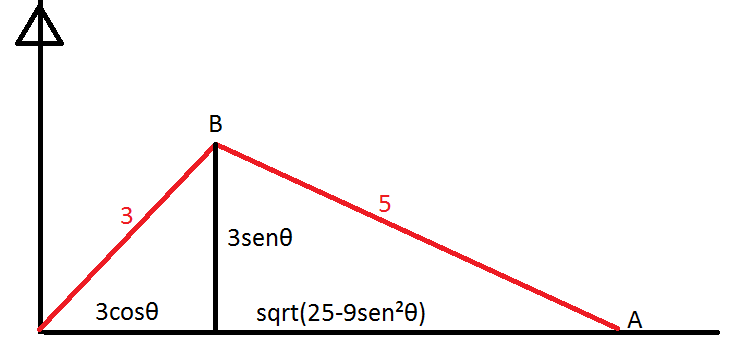
Da figura sabemos que a posição x do ponto A está em função de θ, isto é, x=x(θ), logo, x=3cosθ+sqrt(25-9sen²θ). Além disso, θ está em função do parâmetro t (tempo), isto é, θ=θ(t). Logo, x=x(θ(t)) → dx/dt=(dx/dθ).(dθ/dt). Como:
(dx/dθ)=[3cosθ+sqrt(25-9sen²θ)]'=-3senθ-(9cosθsenθ)/[sqrt(25-9sen²θ)]
(dθ/dt)=(1/2)
Para θ=(π/2)rad tem-se dx/dt=(dx/dθ).(dθ/dt)=(-3)(1/2)=(-3/2)cm/s
Ta certo?

Resposta: (-3/2)cm/s. Essa questão é do livro do prof. Guidorizzi 5ª edição pagina 203
______________________________________________________________________________________________________
Galera, fiz da seguinte forma:

Da figura sabemos que a posição x do ponto A está em função de θ, isto é, x=x(θ), logo, x=3cosθ+sqrt(25-9sen²θ). Além disso, θ está em função do parâmetro t (tempo), isto é, θ=θ(t). Logo, x=x(θ(t)) → dx/dt=(dx/dθ).(dθ/dt). Como:
(dx/dθ)=[3cosθ+sqrt(25-9sen²θ)]'=-3senθ-(9cosθsenθ)/[sqrt(25-9sen²θ)]
(dθ/dt)=(1/2)
Para θ=(π/2)rad tem-se dx/dt=(dx/dθ).(dθ/dt)=(-3)(1/2)=(-3/2)cm/s
Ta certo?

EstudanteCiencias- Jedi

- Mensagens : 358
Data de inscrição : 17/07/2016
Idade : 25
Localização : Salvador - Bahia
 Re: Derivadas
Re: Derivadas
Está certo sim, e muito bem explicado.

Elcioschin- Grande Mestre

- Mensagens : 73172
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












