Comparar nº com raízes da equação do 2º grau

por Cesarr Qui 06 Fev 2014, 12:46

Relembrando a primeira mensagem :

Olá!
Eu estou com dúvida na questão A.244 do livro do Gelson Iezzi vol.1 (é a 3ª edição).

"Determinar m na equação do 2º grau $Comparar nº com raízes da equação do 2º grau - Página 2 Gif$ para que se tenha uma única raiz entre -1 e 2."

Eu pensei assim:

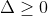
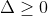
ele quer $Comparar nº com raízes da equação do 2º grau - Página 2 Gif$

Para isso, eu separei assim:

A) -1 < x₁ ≤ x_{2 e}
_B)x₁ ≤ x₂ < 2

E fiz assim:

Para A) Para B)
$Comparar nº com raízes da equação do 2º grau - Página 2 Gif.latex?a$ $Comparar nº com raízes da equação do 2º grau - Página 2 Gif.latex?a$
$Comparar nº com raízes da equação do 2º grau - Página 2 Gif$ $Comparar nº com raízes da equação do 2º grau - Página 2 Gif$
$Comparar nº com raízes da equação do 2º grau - Página 2 Gif$ $Comparar nº com raízes da equação do 2º grau - Página 2 Gif$

Eu calculei todas essas condições para o A) e fiz a intersecção, depois calculei as condições do B) e fiz a intersecção e depois fiz a intersecção de A) e B), porém o meu deu 1/2 < m < 3

Agradeço a quem puder ajudar!

Gabarito:

Spoiler:

por PedroCunha Sáb 08 Fev 2014, 12:15

Show de bola, Cesarr. Excelente trabalho da sua parte. O Fórum agradece.

Abraços,
Pedro

por MatheusFP Seg 28 Mar 2016, 16:34

César, na equação mx^2- 2 (m-1)x +(m+5)=0, a intersecção deve ser feita toda junta ? Tipo; pega todos os valores do primeiro caso é junta com p segundo, Oi resolve separadamente ? Se puder desenvolver a questão iria me ajudar bastante , estou de cabeça quente já , pois não consigo achar o gabarito na hora da intersecção

por **Elcioschin** Seg 28 Mar 2016, 19:27

Sim:

Para x = - 1 ---> f(-1) = m.(-1)² - 2.(m - 1).(-1) - m - 1 ---> f(-1) = 2.m - 3

a.f(-1) < 0 ---> m.(2.m - 3) < 0 ---> 0 < m < 3/2 ---> I

Para x = 2 ---> f(2) = m.2² - 2.(m - 1).2 - m - 1 ---> f(2) = 3 - m

a.f(2) < 0 ---> m.(3 - m) < 0 ---> m < 0 ou m > 3 ---> II

Interseção

............. 0 .............. 3/2 ............... 3 ..........
I: .......... o xxxxxxxxx o ...............................
II xxxxxx o .................................... o xxxxxxx

Solução ---> m < 3/2 com m ≠ 0 e m > 3 --->Mesmo que:

]-∞, 0[ U ]0, 3/2[ U ]3, +∞[

por JoãoLuuz Ter 05 Abr 2022, 19:06

PedroCunha escreveu:Olá.

Se a raiz pertence ao intervalo ]-1,2[, devemos ter m < f(-1) ou m > f(2) e é claro, m ≠ 0:

m*(-1)² - 2 * (m-1) * (-1) - m - 1 .:. m + 2m - 2 - m - 1 .:. 2m - 3 .:. m = 3/2
m*(2)² - 2 * (m-1) * 2 - m - 1 .:. 4m - 4m + 4 - m - 1 .:. m = 3

Logo: m < 3/2 ou m > 3, m ≠ 0

Att.,
Pedro

Boa noite Pedro!

Por que o m < f(-1) ou m > (f2)?