Comparar nº com raízes da equação do 2º grau

por Cesarr Qui 06 Fev 2014, 12:46

Olá!
Eu estou com dúvida na questão A.244 do livro do Gelson Iezzi vol.1 (é a 3ª edição).

"Determinar m na equação do 2º grau $Comparar nº com raízes da equação do 2º grau Gif$ para que se tenha uma única raiz entre -1 e 2."

Eu pensei assim:

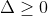
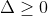
ele quer $Comparar nº com raízes da equação do 2º grau Gif$

Para isso, eu separei assim:

A) -1 < x₁ ≤ x_{2 e}
_B)x₁ ≤ x₂ < 2

E fiz assim:

Para A) Para B)
$Comparar nº com raízes da equação do 2º grau Gif.latex?a$ $Comparar nº com raízes da equação do 2º grau Gif.latex?a$
$Comparar nº com raízes da equação do 2º grau Gif$ $Comparar nº com raízes da equação do 2º grau Gif$
$Comparar nº com raízes da equação do 2º grau Gif$ $Comparar nº com raízes da equação do 2º grau Gif$

Eu calculei todas essas condições para o A) e fiz a intersecção, depois calculei as condições do B) e fiz a intersecção e depois fiz a intersecção de A) e B), porém o meu deu 1/2 < m < 3

Agradeço a quem puder ajudar!

Gabarito:

Spoiler:

por **Elcioschin** Qui 06 Fev 2014, 14:31

Acho que sua interpretação está errada; o enunciado pede que haja apenas UMA raiz entre -1 e 2 e do seu modo existem DUAS raízes no intervalo citado

Acho que o correto então seria

- 1 < x2 < 2 e x1 ≤ - 1

ou

- 1 < x2 < 2 e x1 ≥ 2

Encontre as raízes e imponha estas condições

por Cesarr Qui 06 Fev 2014, 22:05

Obrigado pela atenção, Elcioschin!
Eu entendi o que o senhor falou e fiz, refiz e nada! Muito provavelmente eu esteja errando nos cálculos ou gráficos, pois eu estou aqui desde 8 da manhã fazendo e refazendo esse exercício e posso ter deixado passar algum detalhe por cansaço mesmo. Mas eu também posso estar errando na teoria, por isso eu postei a minha resolução para, se possível, o senhor dar uma olhada e falar onde eu estou errando.

Obs.: Na resolução, eu nem coloquei o delta, pois ele ficou assim: 8m² - 4m + 4, aí, se fizer 8m² - 4m + 4 > 0, o m será qualquer número real, pois a > 0 e delta = -112.

Resolução: casimages.com.br/i/140207124719954271.jpg.html
(Se estiver pequeno, clique na imagem e aperte "F").

Obrigado! Very Happy

por **Elcioschin** Qui 06 Fev 2014, 22:19

Meu caro

Sem o delta você não consegue calcular as raizes
E como vai testar as inequações 0 < x2 e x2 < 2

por PedroCunha Qui 06 Fev 2014, 23:59

Olá.

Se a raiz pertence ao intervalo ]-1,2[, devemos ter m < f(-1) ou m > f(2) e é claro, m ≠ 0:

m*(-1)² - 2 * (m-1) * (-1) - m - 1 .:. m + 2m - 2 - m - 1 .:. 2m - 3 .:. m = 3/2
m*(2)² - 2 * (m-1) * 2 - m - 1 .:. 4m - 4m + 4 - m - 1 .:. m = 3

Logo: m < 3/2 ou m > 3, m ≠ 0

Att.,
Pedro

por Cesarr Sex 07 Fev 2014, 13:12

Muito obrigado, PedroCunha!
Eu nunca teria pensado nisso, pois você fez -1 < x1 < 2 e nem mexeu com o x2, algo que eu não fiz.
Além disso, eu estava calculando -1 < x1 < 2 assim:
a.f(-1) > 0 e a.f(2) > 0
-1 < -b/2a e 2 > -b/2a
delta > 0 e delta > 0
E depois de calcular tudo isso, eu fiz a intersecção.
Mas agora eu aprendi que -1 < x1 < 2 se calcula assim: m < f(-1) ou m > f(2)

Muito obrigado pela ajuda, Elcioschin e PedroCunha!

por PedroCunha Sex 07 Fev 2014, 13:41

Olá.

Esse é um dos casos. É sempre melhor fazer o caminho completo. Podemos ter f(a) < m < f(b) também. Tem que ser feito um estudo pela Teoria mesmo.

Att.,
Pedro

por Cesarr Sex 07 Fev 2014, 20:35

Olá, PedroCunha!

Eu resolvi uns exercícios e consegui deduzir o jeito de resolver para cada caso. Eu estava errando porque eu não sabia que não precisa fazer S/2 <(>) -b/2a quando for do tipo x' < a < x'' < b e do tipo desse exercício aí também.
Mas eu consegui por causa da ajuda de vocês, Elcioschin e PedroCunha!
Agora eu consegui resolver todos os exercícios do livro do Gelson Iezzi desse assunto!

Muitíssimo obrigado! Very Happy

por PedroCunha Sex 07 Fev 2014, 21:34

Cesarr, poste então as conclusões que você chegou acerca da maneira de resolver esse tipo de exercícios. Irá ajudar quem tiver dúvidas.

Att.,
Pedro

por Cesarr Sáb 08 Fev 2014, 09:01

Logo abaixo, estão todos os casos que eu encontrei no livro e como resolvê-los. Eu não sei se esses métodos são corretos, mas funcionaram para todos os exercícios.

CASO: x₁ < 1 < x₂
Determinar m de modo que o número 1 esteja compreendido entre as raízes da equação mx² + (m – 1)x – m = 0.

Resolução:
x₁ < 1 < x₂
a.f(1) < 0
m.(m.1² + (m – 1).1 – m) < 0
m² - m < 0
Agora é só fazer o intervalo.
Resposta: 0 < m < 1

CASO: x₁ < x₂ < 1
Determinar m de modo que a equação (m – 3)x² + 2(m – 2)x + m + 1 = 0 tenha raízes reais tais que x₁ < x₂ < 1.

Resolução:
A)   a.f(1) > 0
(m – 3).(m – 3 + 2m – 4 + m + 1) > 0
4m² - 18m + 18 > 0
m < 3/2 ou m > 3
B)   1 > -b / 2a
1 > -2m + 4 / 2m – 6
-4m + 10 / 2m – 6 < 0
m < 5/3 ou m > 3
C) ∆ > 0
b² - 4.a.c > 0
-8m + 28 > 0
m < 7/2

Agora é só fazer a intersecção entre os intervalos A, B e C.
Resposta: m < 3/2 ou 3 < m < 7/2

CASO: -1 < x₁ < x₂
Determinar m de modo que a equação mx² - (2m + 1)x + 2 + m = 0 tenha raízes reais tais que -1 < x₁ < x₂.

Resolução:
A)   a.f(-1) > 0
m.(m + 2m + 1 + 2 + m) > 0
4m² + 3m > 0
m < -3/4 ou m > 0
B)   -1 < -b / 2a
-1 < 2m + 1 / 2m
4m + 1 / 2m > 0
m < 1/4 ou m > 0
C) ∆ > 0
b² - 4.a.c > 0
-4m + 1 > 0
m < 1/4

Agora é só fazer a intersecção entre os intervalos A, B e C.
Resposta: m < -3/4 ou 0 < m < 1/4

CASO: 0 < x₁ < x₂ < 2
Determinar m de modo que a equação mx² - 2(2m + 1)x + m + 5 = 0 tenha raízes reais tais que 0 < x₁ < x₂ < 2.

Resolução:
Para 0 < x₁ < x₂      Para x₁ < x₂ < 2
a.f(0) > 0               a.f(2) > 0
0 < -b / 2a             2 > -b / 2a
∆ > 0 ∆ > 0

Agora é só calcular tudo e fazer a intersecção.
Resposta: m < -5

CASO: x₁ < 0 < x₂ < 2
Determinar m de modo que a equação mx² - 2(m + 1)x + m + 5 = 0 tenha raízes reais tais que x₁ < 0 < x₂ < 2.

Resolução:
Para x₁ < 0 < x₂     Para 0 < x₂ < 2
a.f(0) < 0              a.f(2) > 0
                           ∆ > 0

Agora é só calcular tudo e fazer a intersecção.
Resposta: -5 < m < -1

CASO: uma única raiz entre dois números.
Determinar m na equação (3m – 2)x² + 2mx + 3m = 0 para que se tenha uma única raiz entre -1 e 0.

Resolução:
-1 < x₁ < 0
m < f(-1) m > f(0)
m < (3m – 2 – 2m + 3)            m > 3m
m < 4m – 2 m > 0
m < 1/2

Resposta: 0 < m < 1/2

É isso aí.