(FESP-SP)P.G.

por Rafael16 Qui 19 Jul 2012, 21:46

Boa noite pessoal,

(FESP-SP) Em um triângulo equilátero de lado L, se unirmos os pontos médios de seus lados obtemos um novo triângulo equilátero. Se procedermos assim sucessivamente obteremos novos triângulos equiláteros, cada vez menores. O limite da soma das áreas dos triângulos equiláteros formados é:

Compreendi isso da seguinte maneira:

$(l,\frac{l}{2},\frac{l}{4},\frac{l}{8},...,\frac{l}{n})$

$S=\frac{l.((\frac{1}{2})^{n-1}-1)}{q-1}$

Não sei como continuar isso...

Resposta: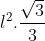 $l^{2}.\frac{\sqrt{3}}{3}$

por **Elcioschin** Qui 19 Jul 2012, 21:55

PG decrescente infinita

Termo S1 da pG ----> S1 = L²*\/3/4

Lado do 2º triângulo = L/2 ----> Termo S2 da PG ----> S2 = (L/2)²*\/3/4 ----> S2 = L²*\/3/16

Razão da PG ----> q = S2/S1 -----> q = (L²*\/3/16)/(L²*\/3/4) ---- q = 1/4

Fórmua da soma dos termos de uma PG infinita decrescente: S = a1/(1 - q)

S = (L²*\/3/4)/(1 - 1/4) -----> S (L²*\/3/4)/(3/4) ----> S = L²*\/3/3

(FESP-SP)P.G.

(FESP-SP)P.G.

Re: (FESP-SP)P.G.

Um fórum livre e democrático.