Trigonometria - intersecção de duas funções
2 participantes
PiR2 :: Matemática :: Trigonometria
Página 1 de 1
Trigonometria - intersecção de duas funções
por Thvilaça Seg 02 Jul 2012, 16:48
(PUC) - O número de pontos de intersecção dos gráficos das funções f e g dadas por: =-\left | cosx \right | "f(x)=-\left | cosx \right |")
e =cos(x+\frac{\pi}{2}) "g(x)=cos(x+\frac{\pi}{2})")
com 
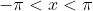, é:
a) 0
b) 1
c) 2
d) 3
e) maior que 3
Resposta: Alternativa c)
Obs.: Só ia pedir pra quem tentasse resolver, mostrasse esses pontos de forma algébrica. Tive dificuldade nessas equações trigonométricas com módulo, e preciso de ajuda, preciso saber como resolver.
Obrigado!
a) 0
b) 1
c) 2
d) 3
e) maior que 3
Resposta: Alternativa c)
Obs.: Só ia pedir pra quem tentasse resolver, mostrasse esses pontos de forma algébrica. Tive dificuldade nessas equações trigonométricas com módulo, e preciso de ajuda, preciso saber como resolver.
Obrigado!
Thvilaça- Recebeu o sabre de luz
- Mensagens : 148
Data de inscrição : 23/06/2011
Localização : São Paulo - SP
Re: Trigonometria - intersecção de duas funções
por Al.Henrique Seg 02 Jul 2012, 18:06
f(x) = g(x)
-|cosx| = cos(x+∏/2)
(I) se cosx > 0 , então :
-cosx = cosx(x+∏/2)
-cosx = -senx
cosx = senx
.'. x = ∏/4 ou x = 5∏/4
ou
(II) se cosx <0 , então :
-cosx = -cos(x+∏/2)
cosx = cos(x+∏/2)
cosx = -senx
Mas como cosx < 0 e -senx < 0 , caimos novamente , no caso (I). Ou seja, serão os mesmos pontos de intersecção.
Para resolver a questão, Bastava lembrar que :
|x| = x , se x>0
|x| = -x , se x<0
-|cosx| = cos(x+∏/2)
(I) se cosx > 0 , então :
-cosx = cosx(x+∏/2)
-cosx = -senx
cosx = senx
.'. x = ∏/4 ou x = 5∏/4
ou
(II) se cosx <0 , então :
-cosx = -cos(x+∏/2)
cosx = cos(x+∏/2)
cosx = -senx
Mas como cosx < 0 e -senx < 0 , caimos novamente , no caso (I). Ou seja, serão os mesmos pontos de intersecção.
Para resolver a questão, Bastava lembrar que :
|x| = x , se x>0
|x| = -x , se x<0
Al.Henrique- Grupo
Velhos amigos do Fórum
- Mensagens : 1203
Data de inscrição : 13/03/2012
Idade : 34
Localização : Rio de Janeiro -
Re: Trigonometria - intersecção de duas funções
por Thvilaça Seg 02 Jul 2012, 18:49
Muito Obrigado mesmo , foi bastante útil.
Se não te incomodasse, eu te faria uma pergunta com relação a funções trigonométricas:
Por exemplo, é possível resolver equações como:
sen(x+5) = sen(x+3), por exemplo, sem recorrer à forma gráfica, só na forma algébrica?
Ou, só é possível resolver na forma algébrica, quando podemos aplicar propriedades trigonométricas, como:
sen(x+(pi/2)) = cos x
cos(x+(pi/2)) = -senx
sen((pi/2)-x) = cos x
cos((pi/2)-x) = senx ???????
Se não te incomodasse, eu te faria uma pergunta com relação a funções trigonométricas:
Por exemplo, é possível resolver equações como:
sen(x+5) = sen(x+3), por exemplo, sem recorrer à forma gráfica, só na forma algébrica?
Ou, só é possível resolver na forma algébrica, quando podemos aplicar propriedades trigonométricas, como:
sen(x+(pi/2)) = cos x
cos(x+(pi/2)) = -senx
sen((pi/2)-x) = cos x
cos((pi/2)-x) = senx ???????
Thvilaça- Recebeu o sabre de luz
- Mensagens : 148
Data de inscrição : 23/06/2011
Localização : São Paulo - SP
Re: Trigonometria - intersecção de duas funções
por Al.Henrique Seg 02 Jul 2012, 19:35
Mas o que fiz foi a forma algébrica..
Na verdade, não motei grafico nenhum.
Você só precisava saber os valores para os quais cosx = senx.
Para um caso mais genérico.
Seja :
Sen(x) = Sen (y)
Pode-se analisar de duas maneiras :
x = y +2k∏
ou
x = ∏ - y +2k∏
Na verdade, não motei grafico nenhum.
Você só precisava saber os valores para os quais cosx = senx.
Para um caso mais genérico.
Seja :
Sen(x) = Sen (y)
Pode-se analisar de duas maneiras :
x = y +2k∏
ou
x = ∏ - y +2k∏
Al.Henrique- Grupo
Velhos amigos do Fórum - Mensagens : 1203
Data de inscrição : 13/03/2012
Idade : 34
Localização : Rio de Janeiro -
Tópicos semelhantes» Intersecção de duas esferas
» Intersecção de duas retas
» Intersecção de Gráficos em Trigonometria
» Dúvida intersecção entre duas retas
» intersecção de funções trigonometricas
» Intersecção de duas retas
» Intersecção de Gráficos em Trigonometria
» Dúvida intersecção entre duas retas
» intersecção de funções trigonometricas
PiR2 :: Matemática :: Trigonometria
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
