Questão EsSA - A área do círculo inscrito em um...
5 participantes
Página 1 de 1
Questão EsSA - A área do círculo inscrito em um...
por Jorge1 Qui 24 maio 2012, 16:58
A área do círculo inscrito em um triângulo retângulo de lados 9, 12 e 15 é:
A) 9pi
B) 4pi
C) pi
D)16pi
E)25pi
A) 9pi
B) 4pi
C) pi
D)16pi
E)25pi
Jorge1- Iniciante
- Mensagens : 19
Data de inscrição : 04/04/2012
Idade : 34
Localização : rj, brasil
Re: Questão EsSA - A área do círculo inscrito em um...
por rihan Qui 24 maio 2012, 17:41
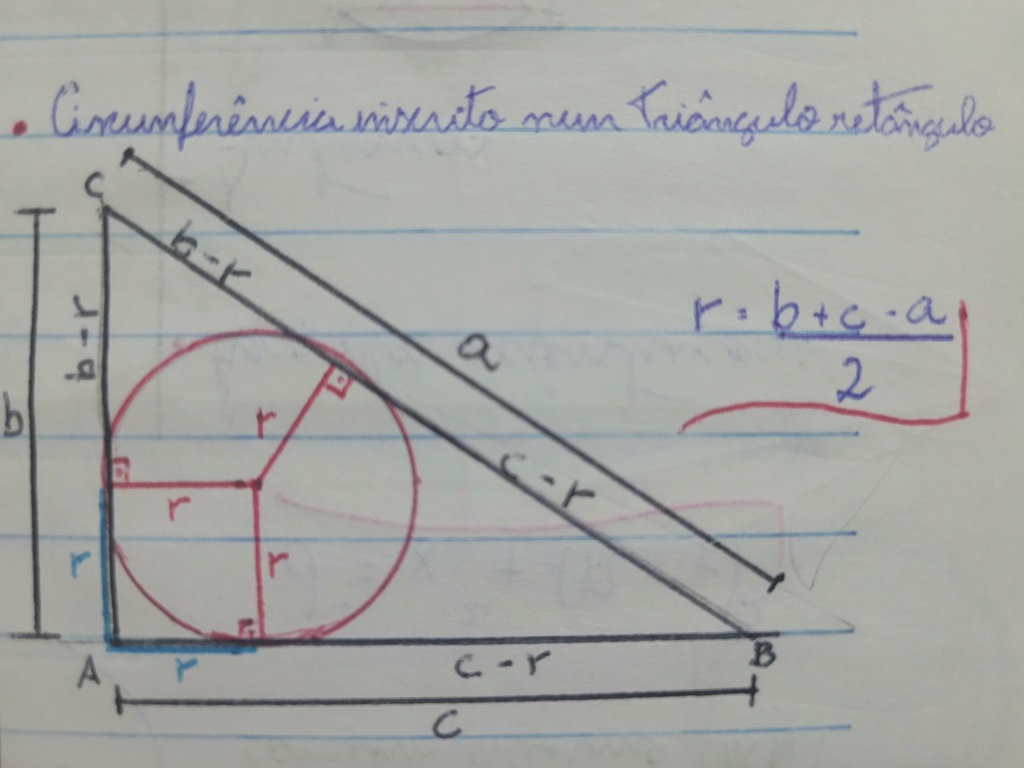
O triângulo (9;12;15) é pitagórico (3;4;5) retângulo.
rihan- Estrela Dourada
- Mensagens : 5049
Data de inscrição : 22/08/2011
Idade : 69
Localização : Rio de Janeiro, RJ, Itabuna-Ilhéus, BA, Brasil
Re: Questão EsSA - A área do círculo inscrito em um...
por CaiqueF Qui 24 maio 2012, 17:52
Ótima resolução rihan.
Eu não conseguiria enxergar isso, rs.
Parabéns
Eu não conseguiria enxergar isso, rs.
Parabéns
CaiqueF- Monitor
- Mensagens : 1237
Data de inscrição : 16/05/2012
Idade : 28
Localização : Salvador -> São Carlos
rihan- Estrela Dourada
- Mensagens : 5049
Data de inscrição : 22/08/2011
Idade : 69
Localização : Rio de Janeiro, RJ, Itabuna-Ilhéus, BA, Brasil
Lucas Padial- Iniciante
- Mensagens : 1
Data de inscrição : 28/04/2023
Re: Questão EsSA - A área do círculo inscrito em um...
por luciano_rael Sex 28 Abr 2023, 10:09
Outra forma de fazer:
Uma fórmula pra calcular a área de um triângulo é: p.r , sendo p o semiperímetro e r o raio da circunferência inscrita ao triângulo
Como ele dá os 3 lados, você poderia descobrir a área pela fórmula de héron:
√p.(p-a)(p-b)(p-c)
√18(9)(6)(3)
√2916 = 54
Ou, sabendo que é um triângulo retângulo, poderia descobrir a área utilizando os catetos: 12.9/2 = 54
voltando à primeira fórmula: 18r = 54
r = 3, Então a área vai ser: pir² = 9pi
Uma fórmula pra calcular a área de um triângulo é: p.r , sendo p o semiperímetro e r o raio da circunferência inscrita ao triângulo
Como ele dá os 3 lados, você poderia descobrir a área pela fórmula de héron:
√p.(p-a)(p-b)(p-c)
√18(9)(6)(3)
√2916 = 54
Ou, sabendo que é um triângulo retângulo, poderia descobrir a área utilizando os catetos: 12.9/2 = 54
voltando à primeira fórmula: 18r = 54
r = 3, Então a área vai ser: pir² = 9pi
luciano_rael- Iniciante
- Mensagens : 12
Data de inscrição : 03/01/2023
Idade : 17
Localização : Rio de Janeiro - RJ
Conteúdo patrocinado
Tópicos semelhantes» Qual a área, em cm², do maior circulo tangente a essa corda e a esse circulo em pontos distintos?
» Area do circulo inscrito no triangulo
» Área do círculo inscrito em um quadrante.
» Área externa de um círculo inscrito
» A área do circulo inscrito no losangulo em cm²
» Area do circulo inscrito no triangulo
» Área do círculo inscrito em um quadrante.
» Área externa de um círculo inscrito
» A área do circulo inscrito no losangulo em cm²
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
