Geometria- Quadrilateros

por TelisLeike Seg 30 Abr 2012, 23:21

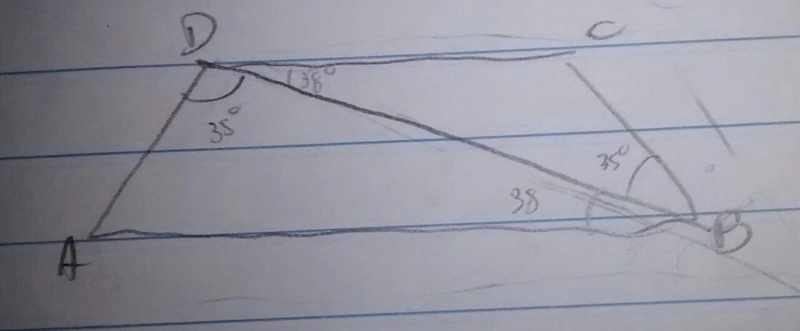
Uma diagonal de um trapezio isosceles forma com uma das bases um angulo de 38° e com um dos lados não paralelo um angulo de 35°. Calcular o menor angulo desse trapezio.

a)53°
b)63°
c)73°
d)83°
e)23°

por profmat2000 Seg 30 Abr 2012, 23:32

por profmat2000 Seg 30 Abr 2012, 23:37

Note que os ângulos BCA e CAD são congruentes, portanto BAD = 35º + 38º = 73º. Como o trapézio é isósceles, os ângulos da base maior são iguais e os ângulos da base menor também são(entre si). Logo ângulo CDA mede 73º.
Por outro lado os ângulos ABC e BCD também são conguruentes - suponhamos de medida x, portanto:
2x + 2 . 73º = 360º ---> 2x + 146º = 360º ---> x = 107º

Portanto os ângulos do trapézio medem 73º, 73º, 107º, 107º e o menor deles mede 73º (alternativa c)

por JEABM Dom 10 Dez 2017, 23:36

Mas se fizer a figura o desenho n bate, pois 107 + 107 ultrapassava 180°....

por **Elcioschin** Dom 10 Dez 2017, 23:52

Você fez o desenho errado

Sejam AB a base maior e CD a base menor ---> Trace a diagonal BD:

A^BD = 38º ---> B^DC = 38º (duas paralelas cortadas por uma transversal)

C^BD = 35º ----> A^BC = A^BD + C^BD ---> A^BC = 38 + 35 --> A^BC = 73º

BÂD = A^BC ---> BÂD = 73º

No triângulo ABD ---> 38º + 73º + A^DB = 180º ---> A^DB = 69º

A^DC = 69º + 38º ---> A^DC = 107º ---> B^CD = 107º

Não há poque somar os dois ângulos de 107º: quem pode ser somado é 107 + 73º = 180º

por JEABM Seg 11 Dez 2017, 00:14

Mas no c^bd o ângulo de 35° n seria duas paralelas cortadas por uma transversal TB? C^bd = a^db = 35°?

por JEABM Seg 11 Dez 2017, 00:22

Esse 107 + 107 confundi c a propriedade do paralelogramo......nos trapézios a + d = 180 e b + c = 180...fiz c + d = 180 e a + b = 180 ( n pode, pois é propriedade dos paralelogramos) xD

por JEABM Seg 11 Dez 2017, 06:16

por **Elcioschin** Seg 11 Dez 2017, 12:40

A transversal BD corta as paralelas AB e CD ---> C^DB = A^BD = 38º

Para o ângulo de 35º NÃO existem duas paralelas cortadas por uma transversal, pois AD não é paralela BC.