Prisma - ITA
4 participantes
Página 1 de 1
Prisma - ITA
por vitorCE Qui 29 Mar 2012, 22:06
Considere um prisma hexagonal regular tal que a razão entre a base a e a aresta lateral l é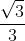 
.
Sabendo que se a aresta da base for aumentada de 2 cm, o volume V do
prisma ficará aumentado de 108 cm³, considerando que a aresta lateral
permanece a mesma, podemos afirmar que o volume do primas é:
Sabendo que se a aresta da base for aumentada de 2 cm, o volume V do
prisma ficará aumentado de 108 cm³, considerando que a aresta lateral
permanece a mesma, podemos afirmar que o volume do primas é:
vitorCE- Mestre Jedi
- Mensagens : 954
Data de inscrição : 24/11/2011
Idade : 29
Localização : Fortaleza
Re: Prisma - ITA
por Medeiros Sáb 31 Mar 2012, 03:28
Antes uma pequena correção: "...tal que a razão entre a aresta da base a e a aresta lateral l é ".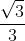
a/L = √3/3 -----> L = a√3
altura do triâng.eq. da base: h = a√3/2
área do triâng. eq. da base: S = a2√3/4
área do hexágono da base: SH = 6S -----> SH = a23√3/2
volume do prisma: V = SHL -----> V = (9/2)a3
a' = a+2 ==> V' = V + 108 -----> V' = (9/2)a3 + 108 ................[I]
h' = (a+2)√3/2
S' = (a+2)2√3/4
S'H = (a+2)23√3/2
V' = (a+2)2(3√3/2)*(a√3)
V' = (9/2)[a2 + 4a + 4]*a
V' = (9/2)[a3 + 4a2 + 4a] ...............[II]
[I] = [II] , vem:
(9/2)[a3 + 4a2 + 4a] = (9/2)a3 + 108
9a3 + 36a2 + 36a - 9a3 - 216 = 0
36a2 + 36a - 216 = 0 ...............................................(÷36)
a2 + a - 6 = 0
--> a = -3 ........... a aresta é um segmento, logo, é positiva ---> não serve
--> a = 2
portanto,
V = (9/2)*23 -----> V = 36 cm3
a/L = √3/3 -----> L = a√3
altura do triâng.eq. da base: h = a√3/2
área do triâng. eq. da base: S = a2√3/4
área do hexágono da base: SH = 6S -----> SH = a23√3/2
volume do prisma: V = SHL -----> V = (9/2)a3
a' = a+2 ==> V' = V + 108 -----> V' = (9/2)a3 + 108 ................[I]
h' = (a+2)√3/2
S' = (a+2)2√3/4
S'H = (a+2)23√3/2
V' = (a+2)2(3√3/2)*(a√3)
V' = (9/2)[a2 + 4a + 4]*a
V' = (9/2)[a3 + 4a2 + 4a] ...............[II]
[I] = [II] , vem:
(9/2)[a3 + 4a2 + 4a] = (9/2)a3 + 108
9a3 + 36a2 + 36a - 9a3 - 216 = 0
36a2 + 36a - 216 = 0 ...............................................(÷36)
a2 + a - 6 = 0
--> a = -3 ........... a aresta é um segmento, logo, é positiva ---> não serve
--> a = 2
portanto,
V = (9/2)*23 -----> V = 36 cm3
Medeiros- Grupo
Velhos amigos do Fórum
- Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
Arquiduque Bartolomeu- Iniciante
- Mensagens : 1
Data de inscrição : 26/03/2013
Idade : 28
Localização : São Luis, Maranhão, Brasil
Re: Prisma - ITA
por VenusianArtist Seg 14 Dez 2015, 10:58
Olá Brother, não consigo entender porque você manteve o "a" sem alteração. Nessa expressão [I] que corresponde ao novo volume, o "a" não deveria estar somado a 2?Medeiros escreveu:
a' = a+2 ==> V' = V + 108 -----> V' = (9/2)a3 + 108 ................[I]
VenusianArtist- Iniciante
- Mensagens : 17
Data de inscrição : 05/11/2015
Idade : 26
Localização : São Paulo-SP, Brasil
Re: Prisma - ITA
por Medeiros Ter 15 Dez 2015, 04:19
Temos um prisma de aresta a e volume V. Inicialmente calculei o volume V.
Quando a aresta é aumentada de 2, temos uma nova aresta a' e um novo volume V'. Então leia essa linha da seguinte forma:
quando temos a', que é igual a (a+2), (==>) então teremos um novo volume V' que é igual a V+108.
Mas V é o volume primevo, calculado antes, e que é função da aresta original a; eu só substituí e assim ficamos com uma equação de V' em função da aresta original a. Até aqui, isto pode ser considerado como dado do problema pois é o que foi dito no enunciado.
Para obter a equação [II], considerei a nova aresta a' no cálculo de V'.
Quando a aresta é aumentada de 2, temos uma nova aresta a' e um novo volume V'. Então leia essa linha da seguinte forma:
quando temos a', que é igual a (a+2), (==>) então teremos um novo volume V' que é igual a V+108.
Mas V é o volume primevo, calculado antes, e que é função da aresta original a; eu só substituí e assim ficamos com uma equação de V' em função da aresta original a. Até aqui, isto pode ser considerado como dado do problema pois é o que foi dito no enunciado.
Para obter a equação [II], considerei a nova aresta a' no cálculo de V'.
Medeiros- Grupo
Velhos amigos do Fórum - Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
