Determine a equação da reta r

Reverse. escreveu:

 Por semelhança até vai mais rápido, mas não é tão elegante quanto a forma do colega acima.

Leonardo Mariano escreveu:Boa tarde.
Montando a equação da reta r:
[latex] y + 1 = m(x - \sqrt{3}) [/latex]
Chamando de A o ponto que fica no eixo x e de B o ponto no eixo y, para encontrar A basta substituir y por 0 na reta, já para B deve ser o x por 0.
[latex] A = (\frac{1 + m\sqrt{3}}{m},0) \: ; \: B = (0,-m\sqrt{3}-1) [/latex]
C é o simétrico de B em relação à origem, como B está no eixo y, basta multiplicar a ordenada de B por -1:
[latex] C = (0, m\sqrt{3}+1) [/latex]
Temos então os 3 pontos em função de m. Para encontrar a equação da reta basta encontrar o valor de m.
Já que o triângulo é equilátero, a distância entre os pontos deve ser a mesma.
Distância BC:
[latex] d^2_{B,C} =(-m\sqrt{3}-1 -m\sqrt{3}-1)^2=(-2m\sqrt{3}-2)^2 [/latex]
Distância AB:
[latex] d^2_{A,B}=(\frac{1 + m\sqrt{3}}{m})^2+(-m\sqrt{3}-1)^2 [/latex]
AB e BC devem ser iguais, mas temos apenas suas distâncias ao quadrado. É possível resolver uma equação do 4 grau, mas para contornar isso vou fazer o seguinte: Dois valores ao quadrado devem ser iguais, logo seus módulos devem ser iguais:
[latex] d^2_{B,C}=d^2_{A,B} \rightarrow |d_{B,C}|=|d_{A,B}| \therefore d_{A,B}=\pm d_{B,C} [/latex]
Fazendo primeiro com o sinal de +:
[latex] (-2m\sqrt{3}-2)^2=(\frac{1 + m\sqrt{3}}{m})^2+(-m\sqrt{3}-1)^2 \\
\rightarrow 4.(-1)^2(m\sqrt{3}+1)^2=(\frac{1 + m\sqrt{3}}{m})^2+(-1)^2(m\sqrt{3}+1)^2  \\
\rightarrow 3(m\sqrt{3}+1)^2=\frac{(1 + m\sqrt{3})^2}{m^2}  \\
\therefore 1+m\sqrt{3}=0 \:\: ou \:\: m^2=\frac{1}{3} \therefore m=\pm \frac{\sqrt{3}}{3} [/latex]
Fazendo o mesmo com o valor negativo chegamos no seguinte:
[latex] -(-2m\sqrt{3}-2)^2=(\frac{1 + m\sqrt{3}}{m})^2+(-m\sqrt{3}-1)^2 \\
\rightarrow -5(m\sqrt{3}+1)^2=\frac{(1 + m\sqrt{3})^2}{m^2}  \\
\therefore 1+m\sqrt{3}=0 \:\: ou \:\: m^2=-\frac{1}{5} \therefore m=\pm \frac{\sqrt{3}}{3} \: ou  \\ m = \pm \frac{\sqrt{5}}{5}i  [/latex]
Com todas as soluções, desconsideramos a imaginária, então sobra ±­ √3/3. Verificando o -√3/3 os pontos ficam todos nulos, então não há um triângulo. Logo, o único valor que é solução do problema é √3/3.
Reta: [latex] y + 1 = \frac{\sqrt{3}}{3}(x - \sqrt{3}) [/latex]
Creio que seja isso, vou colocar o geogebra embaixo para visualização dos pontos de acordo com o valor de m.

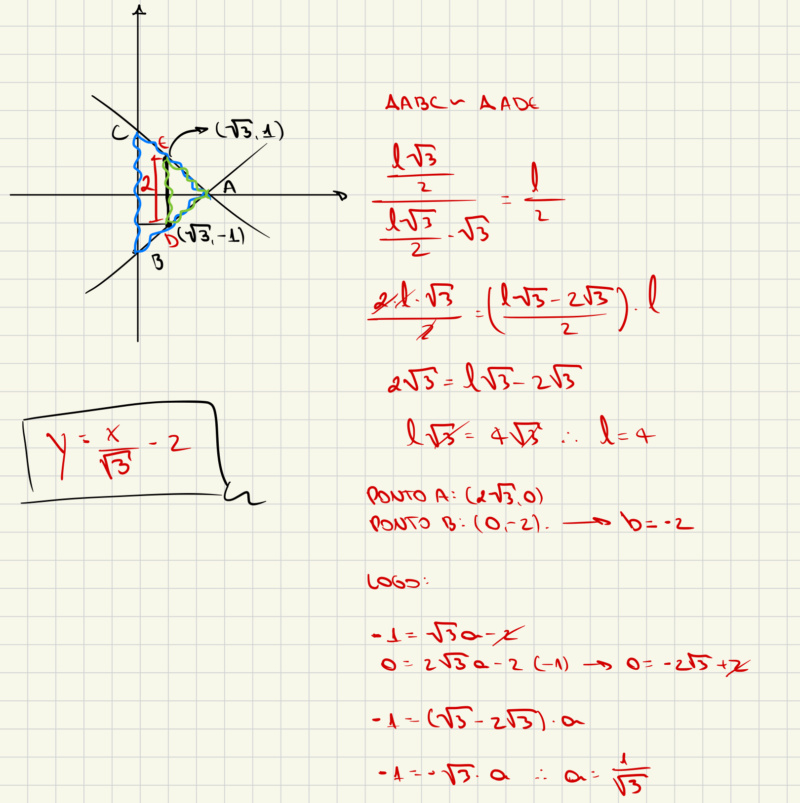
nascelisa escreveu:Boa tarde! Poderia me explicar qual seria a ordem dos segmentos que você está utilizando na fórmula de semelhança de triângulos? Por exemplo AC/AE = CB/ED. Também fiquei com dúvida sobre quem seria o l. Obrigada pela resolução, achei seu raciocínio lógico muito interessante!

Reverse. escreveu:

nascelisa escreveu:Boa tarde! Poderia me explicar qual seria a ordem dos segmentos que você está utilizando na fórmula de semelhança de triângulos? Por exemplo AC/AE = CB/ED. Também fiquei com dúvida sobre quem seria o l. Obrigada pela resolução, achei seu raciocínio lógico muito interessante!

Perdão pelo esquema porco, fiz sua questão quando estava com pressa para um compromisso, mas tentei ajudar mesmo assim. Refiz a parte da sua dúvida: