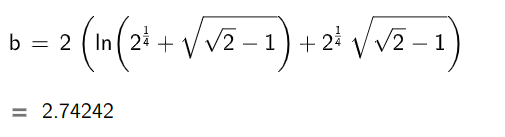Integral definida
2 participantes
Página 1 de 2
Página 1 de 2 • 1, 2 
 Integral definida
Integral definida
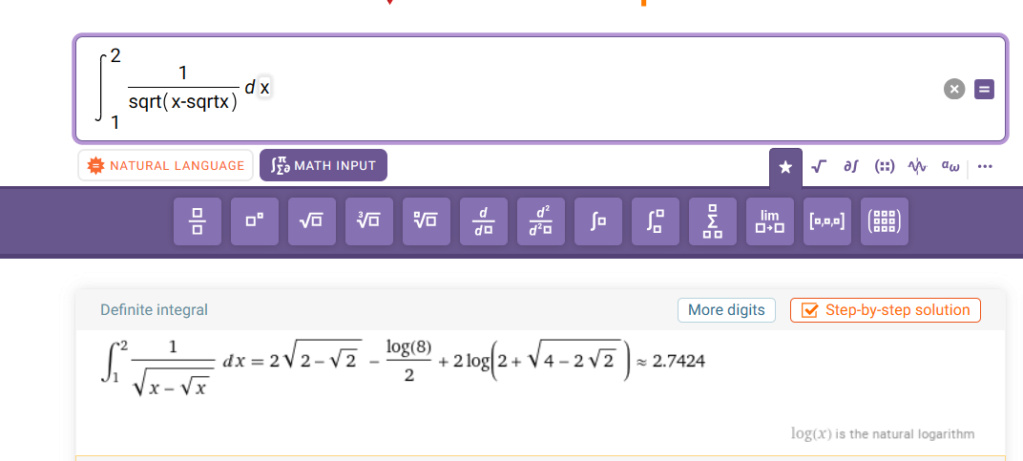
Calcule o valor de [latex]\int_{1}^{2}\frac{1}{\sqrt{x-\sqrt{x}}}dx[/latex].
Resposta: [latex]2(ln(\sqrt[4]{2}+\sqrt{\sqrt{2}-1})+\sqrt[4]{2}\cdot \sqrt{\sqrt{2}-1})[/latex]
Quero ver uma solução bem enxuta para esta integral.
Resposta: [latex]2(ln(\sqrt[4]{2}+\sqrt{\sqrt{2}-1})+\sqrt[4]{2}\cdot \sqrt{\sqrt{2}-1})[/latex]
Quero ver uma solução bem enxuta para esta integral.
Última edição por gsr_principiamathematica em Qua 27 Dez 2023, 19:23, editado 2 vez(es) (Motivo da edição : Colocar o gabarito e corrigir erro na questão.)

gsr_principiamathematica- Padawan

- Mensagens : 50
Data de inscrição : 26/12/2023
Idade : 17
Giovana Martins gosta desta mensagem
 Re: Integral definida
Re: Integral definida
Acho que tem algum problema nesta integral. Se eu não errei contas, note que para x = 0 a integral não é definida, pois teremos um logaritmando negativo. A não ser que estamos lidando com uma integral na variável complexa.
[latex]\\\mathrm{\int \frac{1}{\sqrt{x-\sqrt{x}}}=\int \frac{2u}{\sqrt{u^2-u}}du=\int \left (\frac{2u-1}{2\sqrt{u^2-u}}+\frac{1}{2\sqrt{u^2-u}} \right )du}\\\\ \mathrm{\int \frac{2u-1}{2\sqrt{u^2-u}}du=\int \frac{1}{\sqrt{v}}dv=2\sqrt{u^2-u}}\\\\ \mathrm{\int \frac{1}{2\sqrt{u^2-u}} du=ln\left ( \sqrt{\left ( 2u-1 \right )^2-1}+2u-1 \right )}\\\\ \mathrm{\int \frac{1}{\sqrt{x-\sqrt{x}}}=\sqrt{u^2-u}+\frac{1}{2}ln\left ( \sqrt{\left ( 2u-1 \right )^2-1}+2u-1 \right )}\\\\ \mathrm{Voltando\ em\ x:}\\\\ \mathrm{\int \frac{1}{\sqrt{x-\sqrt{x}}}=2\sqrt{x-\sqrt{x}}+ln\left [ 2\sqrt{x}+\sqrt{\left ( 2\sqrt{x}-1 \right )^2-1}-1\right ]+C}[/latex]
____________________________________________
Charlotte de Witte - Universal Nation

Giovana Martins- Grande Mestre

- Mensagens : 8538
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo
 Re: Integral definida
Re: Integral definida
Mais tarde eu vou mexer mais nas contas. Agora, infelizmente, eu não consigo.
____________________________________________
Charlotte de Witte - Universal Nation

Giovana Martins- Grande Mestre

- Mensagens : 8538
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo
 Re: Integral definida
Re: Integral definida
Mas note que a própria f(x) não é definida para x = 0, então, pensando na integral em termos de área já fica uma coisa incongruente. Não plotei o gráfico ainda, mas a f(x) parece ter uma assíntota nas proximidades de x = 0.
____________________________________________
Charlotte de Witte - Universal Nation

Giovana Martins- Grande Mestre

- Mensagens : 8538
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo
 Re: Integral definida
Re: Integral definida
Giovana, realmente havia um erro na questão. O limite de integração inferior deveria ser 1. Perdão pelo erro.Giovana Martins escreveu:Mas note que a própria f(x) não é definida para x = 0, então, pensando na integral em termos de área já fica uma coisa incongruente. Não plotei o gráfico ainda, mas a f(x) parece ter uma assíntota nas proximidades de x = 0.

gsr_principiamathematica- Padawan

- Mensagens : 50
Data de inscrição : 26/12/2023
Idade : 17
 Re: Integral definida
Re: Integral definida
gsr_principiamathematica escreveu:Giovana, realmente havia um erro na questão. O limite de integração inferior deveria ser 1. Perdão pelo erro.Giovana Martins escreveu:Mas note que a própria f(x) não é definida para x = 0, então, pensando na integral em termos de área já fica uma coisa incongruente. Não plotei o gráfico ainda, mas a f(x) parece ter uma assíntota nas proximidades de x = 0.
Tudo em paz. Não tem problema  . À noite eu tento mexer nela de novo.
. À noite eu tento mexer nela de novo.
____________________________________________
Charlotte de Witte - Universal Nation

Giovana Martins- Grande Mestre

- Mensagens : 8538
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo
 Re: Integral definida
Re: Integral definida
Poxa, ainda assim acho que esta questão tem problemas (ou então é eu que não sei fazer mesmo). Veja o gráfico da f(x).
Note que nem o programa consegue calcular a integral para os limites de integração que vai de 1 até 2, porém, quando os limites de integração vai de 2 até 3 o programa calcula sem problemas. Isso ocorre, porque f(x) não é definida para x = 1 assim como não era para x = 0.
____________________________________________
Charlotte de Witte - Universal Nation

Giovana Martins- Grande Mestre

- Mensagens : 8538
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo

gsr_principiamathematica- Padawan

- Mensagens : 50
Data de inscrição : 26/12/2023
Idade : 17
Giovana Martins gosta desta mensagem
 Re: Integral definida
Re: Integral definida
Bom, então eu vou seguir no que eu havia dito antes de que eu que não sei fazer a questão kkkk.
Amanhã eu vou tentar mexer mais um pouco nessa conta. Agora já está tarde. Já passou e muito do horário de eu ir dormir.
Olhando a expressão que o Wolfram chegou, parece que está diferente da minha. Talvez eu tenha errado contas.
____________________________________________
Charlotte de Witte - Universal Nation

Giovana Martins- Grande Mestre

- Mensagens : 8538
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo
 Re: Integral definida
Re: Integral definida
Na verdade eu falei uma enorme bobagem. Fui fazendo as contas de cabeça e por isso que eu errei.
A expressão que eu cheguei ali é diferente da do Wolfram, mas substituindo os limites de integração na expressão que eu cheguei, o gabarito bate com o seu.
E para x = 1 a integral vai a zero.

Giovana Martins- Grande Mestre

- Mensagens : 8538
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo
gsr_principiamathematica gosta desta mensagem
Página 1 de 2 • 1, 2 
Página 1 de 2
Permissões neste sub-fórum
Não podes responder a tópicos