Tangentes horizontais.
4 participantes
Página 1 de 2
Página 1 de 2 • 1, 2 
 Tangentes horizontais.
Tangentes horizontais.
Encontre uma função cúbica y = ax³ + bx² + cx + d cujo gráfico tenha tangentes horizontais nos pontos (-2,6) e (2,0).
Resp.: Sem gabarito.
Boaa noite amigos!
Então fiquei com dúvida nessa questão pois aprendi que, quando queremos achar retas tangentes a curvas, podemos fazer o seguinte:
1. Derivar y
2. Jogar o "x" do ponto de tangência para descobrir a inclinação da reta.
3. Após isso, substituir tudo em: y = m(x - x0) + y0
Porém, quando me deparei com essa questão, eu me embolei...
Pois ele diz que a tangente deve ser horizontal, ou seja, m = 0...
Só que, quando derivamos, devemos substituir "y" pelo ponto dado...
Ou seja, me embolei todo.
No que estou errando?
Vlww!
Resp.: Sem gabarito.
Boaa noite amigos!
Então fiquei com dúvida nessa questão pois aprendi que, quando queremos achar retas tangentes a curvas, podemos fazer o seguinte:
1. Derivar y
2. Jogar o "x" do ponto de tangência para descobrir a inclinação da reta.
3. Após isso, substituir tudo em: y = m(x - x0) + y0
Porém, quando me deparei com essa questão, eu me embolei...
Pois ele diz que a tangente deve ser horizontal, ou seja, m = 0...
Só que, quando derivamos, devemos substituir "y" pelo ponto dado...
Ou seja, me embolei todo.
No que estou errando?
Vlww!
Última edição por Bergamotinha OwO em Dom 03 Abr 2022, 14:32, editado 1 vez(es)

Bergamotinha OwO- Recebeu o sabre de luz

- Mensagens : 112
Data de inscrição : 25/10/2021
Localização : Pé de laranjeira, Brasil
 Re: Tangentes horizontais.
Re: Tangentes horizontais.
Fiz assim, ficou grandão kkk
I) 0 = 8a + 4b + 2c + d
II) 6 = -8a + 4b - 2c + d
I + II)
8b + 2d = 6
4b + d = 3
I - II)
16a + 4c = -6
8a + 2c = -3
Além disso, uma das raízes é o 2
Utilizando Girard:
I) 2 + r1 + r2 = -b / a
r1 + r2 = -b/a - 2
II) r1 . r2 . 2= -d/a
r1 . r2 = -d / 2a
III) r1 . r2 + 2r2 + 2 r1 = c / a
Substituindo I e II em III
-d / 2a + 2. (r1 + r2) = c / a
-d / 2a + 2 . (-b/a - 2) = c / a
- d / 2a - 2b/a - 4 = c / a
-d / 2 - 2b - 4 = c
-d - 4b - 8 = 2c
-d - 4b = 2c + 8
-d - 4b = -3
d + 4b = 3
Editei aqui, Gi. Acabei chegando na mesma coisa de antes
I) 0 = 8a + 4b + 2c + d
II) 6 = -8a + 4b - 2c + d
I + II)
8b + 2d = 6
4b + d = 3
I - II)
16a + 4c = -6
8a + 2c = -3
Além disso, uma das raízes é o 2
Utilizando Girard:
I) 2 + r1 + r2 = -b / a
r1 + r2 = -b/a - 2
II) r1 . r2 . 2= -d/a
r1 . r2 = -d / 2a
III) r1 . r2 + 2r2 + 2 r1 = c / a
Substituindo I e II em III
-d / 2a + 2. (r1 + r2) = c / a
-d / 2a + 2 . (-b/a - 2) = c / a
- d / 2a - 2b/a - 4 = c / a
-d / 2 - 2b - 4 = c
-d - 4b - 8 = 2c
-d - 4b = 2c + 8
-d - 4b = -3
d + 4b = 3
Editei aqui, Gi. Acabei chegando na mesma coisa de antes
Última edição por gusborgs em Dom 03 Abr 2022, 02:29, editado 2 vez(es)

gusborgs- Mestre Jedi

- Mensagens : 715
Data de inscrição : 27/08/2021
Giovana Martins e Bergamotinha OwO gostam desta mensagem
 Re: Tangentes horizontais.
Re: Tangentes horizontais.
Acho que é isso.
[latex]\\\mathrm{Tangente\ horizontal\to \frac{dy}{dx}=0}\\\\ \mathrm{\frac{dy}{dx}=\frac{d}{dx}(ax^3 + bx^2 + cx + d)=3ax^2+2bx+c=0}\\\\ \mathrm{No\ ponto\ (2,0):12a+4b+c=0\ (I)}\\\\ \mathrm{No\ ponto\ (-2,6):12a-4b+c=0\ (II)}\\\\ \mathrm{(-2,6)\in y = ax^3 + bx^2 + cx + d \ \therefore \ -8a+4b-2c+d=6\ (III)}\\\\ \mathrm{(2,0)\in y = ax^3 + bx^2 + cx + d \ \therefore \ 8a+4b+2c+d=0\ (IV)}\\\\ \mathrm{Do\ sistema:(a,b,c,d)=\left ( \frac{3}{16},0,-\frac{9}{4},3 \right )\ \therefore \ y=\frac{3}{16}x^3-\frac{9}{4}x+3}\\\\ \mathrm{Teste:\frac{dy}{dx}(2,0)=\frac{9}{16}\times (2)^2-\frac{9}{4}=0\to Ok!}\\\\ \mathrm{Teste:\frac{dy}{dx}(-2,6)=\frac{9}{16}\times (-2)^2-\frac{9}{4}=0\to Ok!}[/latex]
Ilustração gráfica:
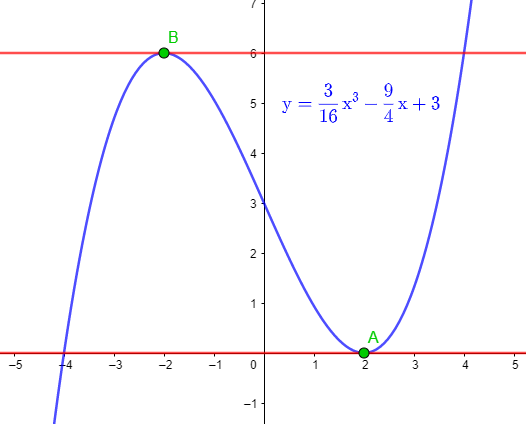
[latex]\\\mathrm{Tangente\ horizontal\to \frac{dy}{dx}=0}\\\\ \mathrm{\frac{dy}{dx}=\frac{d}{dx}(ax^3 + bx^2 + cx + d)=3ax^2+2bx+c=0}\\\\ \mathrm{No\ ponto\ (2,0):12a+4b+c=0\ (I)}\\\\ \mathrm{No\ ponto\ (-2,6):12a-4b+c=0\ (II)}\\\\ \mathrm{(-2,6)\in y = ax^3 + bx^2 + cx + d \ \therefore \ -8a+4b-2c+d=6\ (III)}\\\\ \mathrm{(2,0)\in y = ax^3 + bx^2 + cx + d \ \therefore \ 8a+4b+2c+d=0\ (IV)}\\\\ \mathrm{Do\ sistema:(a,b,c,d)=\left ( \frac{3}{16},0,-\frac{9}{4},3 \right )\ \therefore \ y=\frac{3}{16}x^3-\frac{9}{4}x+3}\\\\ \mathrm{Teste:\frac{dy}{dx}(2,0)=\frac{9}{16}\times (2)^2-\frac{9}{4}=0\to Ok!}\\\\ \mathrm{Teste:\frac{dy}{dx}(-2,6)=\frac{9}{16}\times (-2)^2-\frac{9}{4}=0\to Ok!}[/latex]
Ilustração gráfica:

____________________________________________
Charlotte de Witte - Universal Nation

Giovana Martins- Grande Mestre

- Mensagens : 8526
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo
gusborgs e Bergamotinha OwO gostam desta mensagem
 Re: Tangentes horizontais.
Re: Tangentes horizontais.
Oii, gusborgs. Acho que chegamos em valores diferentes. Vou rever as minhas contas  .
.
____________________________________________
Charlotte de Witte - Universal Nation

Giovana Martins- Grande Mestre

- Mensagens : 8526
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo
gusborgs e Bergamotinha OwO gostam desta mensagem
 Re: Tangentes horizontais.
Re: Tangentes horizontais.
Ja editei Gi, acabei chegando na mesma igualdade 

gusborgs- Mestre Jedi

- Mensagens : 715
Data de inscrição : 27/08/2021
Giovana Martins e Bergamotinha OwO gostam desta mensagem
 Re: Tangentes horizontais.
Re: Tangentes horizontais.
gusborgs escreveu:Fiz assim, ficou grandão kkk
I) 0 = 8a + 4b + 2c + d
II) 6 = -8a + 4b - 2c + d
I + II)
8b + 2d = 6
4b + d = 3
I - II)
16a + 4c = -6
8a + 2c = -3
Além disso, uma das raízes é o 2
Utilizando Girard:
I) 2 + r1 + r2 = -b / a
r1 + r2 = -b/a - 2
II) r1 . r2 . 2= -d/a
r1 . r2 = -d / 2a
III) r1 . r2 + 2r2 + 2 r1 = c / a
Substituindo I e II em III
-d / 2a + 2. (r1 + r2) = c / a
-d / 2a + 2 . (-b/a - 2) = c / a
- d / 2a - 2b/a - 4 = c / a
-d / 2 - 2b - 4 = c
-d - 4b - 8 = 2c
-d - 4b = 2c + 8
-d - 4b = -3
d + 4b = 3
Editei aqui, Gi. Acabei chegando na mesma coisa de antes
Ah, creio que ao fazer "I+II" e "I-II" você caiu em um sistema redundante (há dependência entre as matrizes dessas equações). Para que um sistema seja determinado e existente não pode haver redundância, isto é, não pode haver dependência entre as equações.
____________________________________________
Charlotte de Witte - Universal Nation

Giovana Martins- Grande Mestre

- Mensagens : 8526
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo
gusborgs e Bergamotinha OwO gostam desta mensagem
 Re: Tangentes horizontais.
Re: Tangentes horizontais.
Olá gente!
Bom dia!
Vlww pelas ajudas! Consegui compreender!
Então, com isso, eu posso continuar a usar o método q aprendi?
De tipo, derivar a função dada; dps substituir pela abscissa do ponto dado e descobrir a inclinação da reta; e dps disso jogar naquela fórmula.
Ou vcs me recomendariam outro tipo de método?
Bom dia!
Vlww pelas ajudas! Consegui compreender!
Então, com isso, eu posso continuar a usar o método q aprendi?
De tipo, derivar a função dada; dps substituir pela abscissa do ponto dado e descobrir a inclinação da reta; e dps disso jogar naquela fórmula.
Ou vcs me recomendariam outro tipo de método?

Bergamotinha OwO- Recebeu o sabre de luz

- Mensagens : 112
Data de inscrição : 25/10/2021
Localização : Pé de laranjeira, Brasil
 Re: Tangentes horizontais.
Re: Tangentes horizontais.
Bergamotinha OwO escreveu:Olá gente!
Bom dia!
Vlww pelas ajudas! Consegui compreender!
Então, com isso, eu posso continuar a usar o método q aprendi?
De tipo, derivar a função dada; dps substituir pela abscissa do ponto dado e descobrir a inclinação da reta; e dps disso jogar naquela fórmula.
Ou vcs me recomendariam outro tipo de método?
Tudo o que você falou está correto, entretanto, aqui temos um caso particular de uma tangente horizontal sem contar que a função polinomial que a gente dispõe não está previamente definida já que os seus coeficientes (a, b, c, d) é parte do que precisamos solucionar.
____________________________________________
Charlotte de Witte - Universal Nation

Giovana Martins- Grande Mestre

- Mensagens : 8526
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo
Bergamotinha OwO gosta desta mensagem
 Re: Tangentes horizontais.
Re: Tangentes horizontais.
Ahh sim, compreendi!
Brigadão Gi e Gusborgs pela ajuda!
Apenas mais uma coisinha só, que me veio na cabeça agr: retas tangentes a curvas e retas normais a curvas são as mesmas coisas? Seria apenas uma denominação diferente para coisas iguais ou são conceitos diferentes?
Brigadão Gi e Gusborgs pela ajuda!
Apenas mais uma coisinha só, que me veio na cabeça agr: retas tangentes a curvas e retas normais a curvas são as mesmas coisas? Seria apenas uma denominação diferente para coisas iguais ou são conceitos diferentes?

Bergamotinha OwO- Recebeu o sabre de luz

- Mensagens : 112
Data de inscrição : 25/10/2021
Localização : Pé de laranjeira, Brasil
Giovana Martins gosta desta mensagem
 Re: Tangentes horizontais.
Re: Tangentes horizontais.
São coisas diferentes.
Reta tangente à curva: são as retas em vermelho que eu indiquei na figura acima.
Reta normal à curva: é uma reta perpendicular à curva, por exemplo, duas retas se intersectando sob um ângulo reto (90°).
Um exemplo de ambas as situações:

Fonte: https://www.alfaconnection.pro.br/matematica/geometria/circunferencia-elipse-hiperbole-e-parabola/elementos-e-nomenclatura-da-elipse/
Reta tangente à curva: são as retas em vermelho que eu indiquei na figura acima.
Reta normal à curva: é uma reta perpendicular à curva, por exemplo, duas retas se intersectando sob um ângulo reto (90°).
Um exemplo de ambas as situações:

Fonte: https://www.alfaconnection.pro.br/matematica/geometria/circunferencia-elipse-hiperbole-e-parabola/elementos-e-nomenclatura-da-elipse/
____________________________________________
Charlotte de Witte - Universal Nation

Giovana Martins- Grande Mestre

- Mensagens : 8526
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo
Bergamotinha OwO gosta desta mensagem
Página 1 de 2 • 1, 2 
 Tópicos semelhantes
Tópicos semelhantes» Tangentes horizontais à curva
» Retas Horizontais e Verticais
» Assíntotas horizontais
» Verifique se há assíntotas horizontais
» tangentes
» Retas Horizontais e Verticais
» Assíntotas horizontais
» Verifique se há assíntotas horizontais
» tangentes
Página 1 de 2
Permissões neste sub-fórum
Não podes responder a tópicos












