Geometria Plana- Triangulo retângulo

por makarow Ter 27 Jul - 19:45

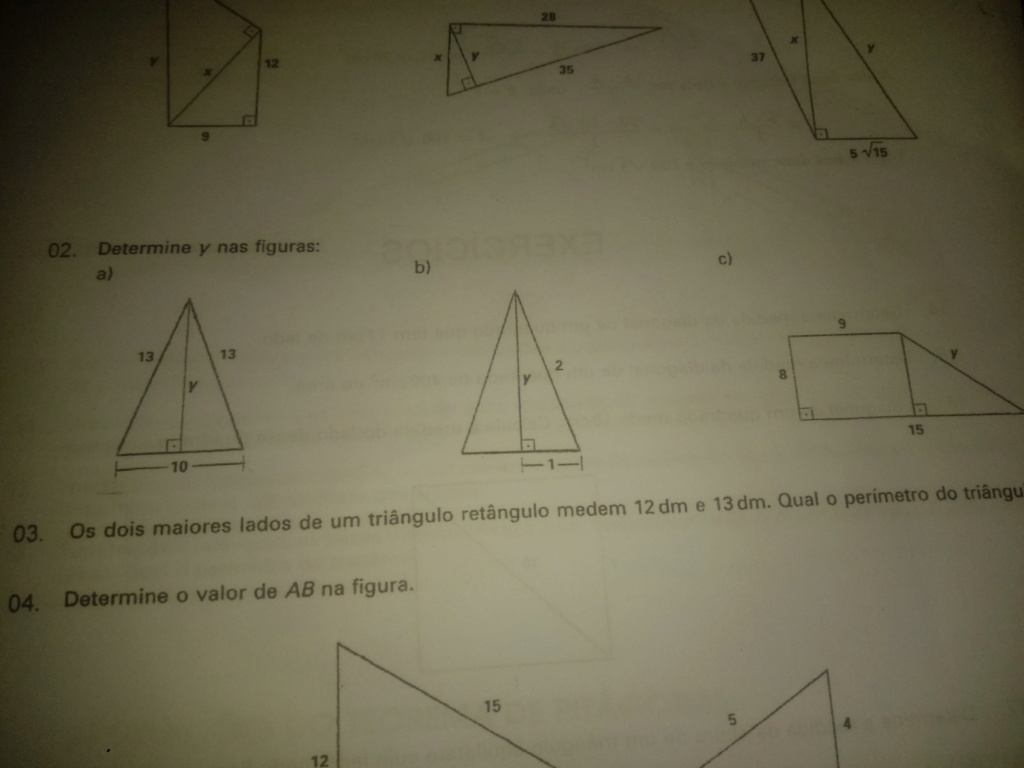
É o número 2 e a questão é a letra A

por **Rory Gilmore** Ter 27 Jul - 20:47

É só aplicar o Teorema de Pitágoras.

por SO_Manetol Ter 27 Jul - 22:11

Oi, como vai. Deixando a minha contribuição no tópico.

- Trata-se da altura de um lado do triângulo, adotando os pontos A, B e C no sentido anti-horário, logo temos de determinar a altura de A. Para tal, utilizamos a fórmula:

hA= 1/BC . V [p. (p - AB). (p-BC). (p- AC)]

p - Semiperímetro do triângulo

por **Medeiros** Qua 28 Jul - 0:18

complementando o dito pela Rory.

como o triângulo tem duas pernas de medida 13, trata-se de um triânguloo isósceles. Sendo isósceles, a altura (pois há um ângulo reto) traçada desse vértice é também a mediatriz da base; e assim sendo a divide ao meio, logo cada pedaço da base mede 5 unidades. Isto significa que esse triângulo isósceles pode ser considerado como dois triângulos retângulos de catetos 5 e y e de hipotenusa 13.

por **MarioCastro** Qua 28 Jul - 1:38

SO_Manetol escreveu:Oi, como vai. Deixando a minha contribuição no tópico.

- Trata-se da altura de um lado do triângulo, adotando os pontos A, B e C no sentido anti-horário, logo temos de determinar a altura de A. Para tal, utilizamos a fórmula:

hA= 1/BC . V [p. (p - AB). (p-BC). (p- AC)]

p - Semiperímetro do triângulo

Usou bomba nuclear para cavar uma cova lol!