Interseção entre uma função e sua inversa

por Fëanor Sex 21 maio 2021, 20:13

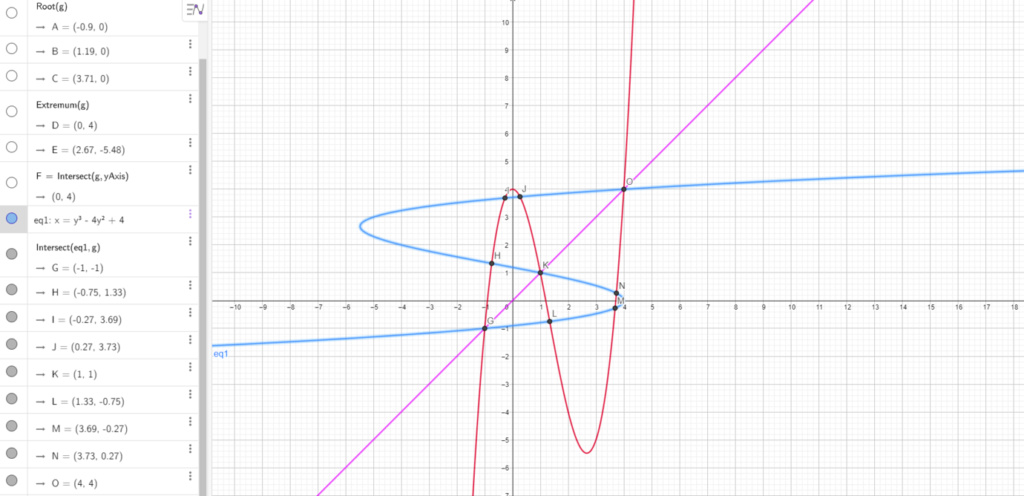
Seja [latex]f:\mathbb{R}\rightarrow \mathbb{R}[/latex] uma função dada por [latex]f(x)=x^{3}-4x^{2}+4[/latex].

A soma das abscissas dos pontos de interseção dos gráficos dessa função e de sua relação inversa é

a) 0.
b) 1.
c) 2.
d) 3.
e) Maior que 3.

Minha tentativa:

Seja [latex]I(x)=x[/latex] a função identidade, note que se [latex]\exists a : f(a)=a[/latex] , e f possui uma inversa, temos que [latex]f^{-1}(a)=a[/latex]

Assim, [latex](a,a)\in I(x)\wedge (a,a)\in f(x)\wedge (a,a)\in f^{-1}(x)[/latex] e [latex](a,a)[/latex] é um ponto de interseção de [latex]f(x)[/latex] , [latex]f^{-1}(x)[/latex] e [latex]I(x)[/latex] , ou seja, dado que existe uma interseção entre a função [latex]f(x)[/latex] e a funnção identidade, pelo menos um ponto de interseção entre [latex]f(x)[/latex] e sua inversa caem sobre a própria função identidade.

Fazendo [latex]f(x)=x[/latex] , temos que

[latex]x^{3}-4x^{2}-x+4=0[/latex] ,logo:

[latex]x=4 \veebar x=1 \veebar x=-1[/latex]

Portanto temos que nos pontos [latex](4,4) ,(1,1),(-1,-1)[/latex] a função e sua inversa interceptam-se, note que não há garantia que estes são os únicos pontos que isto ocorre. Sendo S a soma das abscissas os pontos de interseção dos gráficos dessa função e de sua relação inversa teremos que : [latex]S=4+1-1+k[/latex] onde k é a soma das outras possíveis abscissas.

[latex]S=4+1-1+k[/latex], se [latex]k>0[/latex] então [latex]S>4[/latex] e a alternativa e é correta, porém, se [latex]k<0[/latex] a análise é inconclusiva. Como posso determinar k ? Existe uma maneira mais simles de resolver este problema ?

por Dimizkaz Sex 21 maio 2021, 20:57

Bom, vou te mostrar o modo como eu pensei

Considerando que uma função e sua inversa são sempre simétricas, veja um exemplo abaixo:

Interseção entre uma função e sua inversa A7thyhq8P7AvAAAAAElFTkSuQmCC

Interseção entre uma função e sua inversa A7thyhq8P7AvAAAAAElFTkSuQmCC

o ponto de encontro delas, tem que ser necessariamente algo assim (X,Y) com Y=X, pois o único lugar para intersecção é o eixo de simetria.

Tendo isso em mente, os pontos de intersecção serão da forma(x,x), portanto:

F(x)=x^3-4X^2+4=x

resolvendo isso teremos:
(X^2-1)(X-4)=0
o que é exatamente os pontos (1,1) (-1,-1) e (4,4) que vc já encontrou, portanto a soma dá 4, eu não entendi esse K que vc colocou, para falar a verdade, não entendi muito o que vc fez, talvez isso te ajude, ou não.

por Dimizkaz Sex 21 maio 2021, 21:03

Acho que o eixo de simetria garante que elas são os únicos, não?

por Fëanor Sex 21 maio 2021, 21:38

Dimizkaz escreveu:Bom, vou te mostrar o modo como eu pensei

Considerando que uma função e sua inversa são sempre simétricas, veja um exemplo abaixo:

o ponto de encontro delas, tem que ser necessariamente algo assim (X,Y) com Y=X, pois o único lugar para intersecção é o eixo de simetria.

Tendo isso em mente, os pontos de intersecção serão da forma(x,x), portanto:

F(x)=x^3-4X^2+4=x

resolvendo isso teremos:
(X^2-1)(X-4)=0
o que é exatamente os pontos (1,1) (-1,-1) e (4,4) que vc já encontrou, portanto a soma dá 4, eu não entendi esse K que vc colocou, para falar a verdade, não entendi muito o que vc fez, talvez isso te ajude, ou não.

É errado assumir que o único lugar possível de interseção de uma função e sua inversa seja sobre a bissetriz do primeiro quadrante. Por exemplo, tomemos duas funções [latex]g:\mathbb{R}\rightarrow \mathbb{R}[/latex] e [latex]j:\mathbb{R}-\left \{ 0 \right \}\rightarrow \mathbb{R}-\left \{ 0 \right \}[/latex], onde [latex]g(x)=-x[/latex] e [latex]j(x)=\frac{1}{x}[/latex] .

Note que :

[latex]g^{-1}(x)=-x=g(x)[/latex]

[latex]j^{-1}(x)=\frac{1}{x}=j(x)[/latex]

Assim, existem infinitos pontos onde estas funções interceptam suas inversas

Se fosse verdade que a interseção só é possível sobre y=x, teríamos que

[latex]g(x)=x[/latex] e [latex]j(x)=x[/latex] nos dão os únicos pontos onde as funções interceptam suas inversas.

[latex]g(x)=x\rightarrow -x=x\rightarrow 2x=0\rightarrow x=0 [/latex].Assim, [latex](0,0)[/latex] seria o único ponto de interseção entre g e sua inversa o que é um absurdo.

[latex]j(x)=x\rightarrow \frac{1}{x}=x\rightarrow x^{2}=1\rightarrow (x-1)(x+1)=0\rightarrow x=1\veebar x=-1[/latex]. Assim, [latex](1,1),(-1,-1)[/latex] seriam os únicos pontos de interseção entre j e sua inversa o que é um absurdo.

Estes 3 pontos que encontrei pertencem a interseção de [latex]f(x)[/latex] e sua inversa, porém, perceba que nada garante que estes sejam os únicos pontos de interseção. K seria a soma das abscissas dos demais pontos de interseção.

por Fëanor Sex 21 maio 2021, 22:06

Dimizkaz escreveu:Acho que o eixo de simetria garante que elas são os únicos, não?

Interseção entre uma função e sua inversa F_inv210

Observe que pelo gráfico de f(x) e sua inversa existem 9 pontos de interseção

por Dimizkaz Sex 21 maio 2021, 22:32

Agr compreendo, é realmente absurdo assumir isso
Foi até ingênuo eu ter assumido
Não consigo pensar em outra forma de encontrar as outras intersecções, a não ser encontrando a própria função inversa e igualando, nem sei mais se isso daria certo, considerando minhas falsas afirmações anteriores.
Bom, acho que teremos que esperar alguma mente mais acostumadas nesses assuntos.

por jonathan333 Seg 18 Nov 2024, 19:42

Opa, sei que o tópico é antigo mas me deparei com esse problema também e consegui visualizar um modo de encontrar o gabarito da questão e algumas outras raízes "escondidas".

Queremos a soma das abscissas de [latex]f\left(x\right)=f^{-1}\left(x\right)[/latex].

Seguindo de forma padrão;
[latex]x^3-4x^2+4=x[/latex] se e somente se [latex]x\left(x^2-1\right)=4\left(x^2-1\right)[/latex]

[latex]x=-1, x=1[/latex] ou [latex]x=4[/latex]

Mas não acaba por aqui, pode ser que ainda temos outros pontos de interseção, já que não sabemos qual é a função inversa precisamos assumir isso;

[latex]f\left(x\right)=f^{-1}\left(x\right)[/latex] ⇔ [latex]f\left(f^{-1}\left(x\right)\right)=x[/latex]

[latex]f\left(x\right)^3-4f\left(x\right)^2+4=x[/latex] ⇒ [latex]\left(x^3-4x^2+4\right)^3-4\left(x^3-4x^2+4\right)^2=x-4[/latex]
[latex]\left(x^3-4x^2+4\right)^2\left[x^2\left(x-4\right)\right]=\left(x-4\right)[/latex]
Daqui, temos que: [latex]x=4[/latex], [latex]x^4-4x^3+4x=1[/latex] ou [latex]x^4-4x^3+4x=-1[/latex]

Resolvendo para [latex]x^4-4x^3+4x=1[/latex];
[latex]x^4-1=4x^3-4x[/latex] ⇒ [latex]\left(x^2-1\right)\left(x^2+1\right)=4x\left(x^2-1\right)[/latex]
x=1, x=-1 (que ja tínhamos encontrado) ou [latex]x^2-4x+1=0[/latex] ⇒ x=2±√3

Mas ainda temos o caso [latex]x^4-4x^3+4x=-1[/latex] que é bem mais complicado a análise, jogando a equação no wolfram alpha, encontramos as 4 raízes reais dessa equação, mas vamos tentar encontrar na mão;

[latex]x^4+1=4x\left(x^2-1\right)[/latex]
vamos separar em casos, fazendo [latex]x\le -1[/latex] ⇒ [latex]4x\left(x^2-1\right)\le 0[/latex] mas nesse caso chegamos a um absurdo, ja que
[latex]x^4+1\le 0[/latex] e é impossível isso ser menor do que zero. (sem solução)

Fazendo -1 < x < 0 ⇒ [latex]\left|x\left(x+1\right)\right|\le \left|\frac{1}{4}\right|[/latex]
[/latex]\left(2x+1\right)^2>0[/latex] ⇒ [latex]4x^2+4x+1\ge 0[/latex] ⇒ [latex]4x\left(x+1\right)\ge -1[/latex] ⇒ [latex]-\frac{1}{4}\le x\left(x+1\right)\le 0[/latex]

[latex]x^4+1=\left(1-x\right)\left(1+x\right)x[/latex] ⇒ [latex]x^4+1=\left(1-x\right)\left[4\left(-x\right)\left(1+x\right)\right][/latex] Dessa forma, fica evidenciado o valor do módulo de 1/4 que eu criei na linha acima, permitindo-nos afirmar que; [latex]\left(1-x\right)\left[4\left(-x\right)\left(1+x\right)\right]\ge 1-x[/latex] ⇒ [latex]x^4\ge -x[/latex] ⇒ [latex]\left(-x\right)\left(-x\right)^3\ge -x[/latex] ⇒ [latex]x^3\le -1[/latex]
⇒ [latex]x\le -1[/latex] o que é um absurdo.

Agora faltaria analisar o caso [latex]x\ge \:0[latex], o que foge do meu intelecto resolver esse caso, mas a conclusão que tiramos dessa análise é:
Seja S o nosso conjunto solução [latex]S=\left\{-1,\:2-\sqrt{3},\:1,\:2+\sqrt{3},\:4,\:,j\right\}[/latex]
Aonde j é alguma outra raiz positiva que tiraríamos do caso x≥0, a soma de todos os termos do conjunto S é igual a (8+j), j≥0.

Concluindo gabarito letra E) Maior que 3.