Número complexo.

por **Eduardo Rabelo** Qua 26 Ago 2020, 10:04

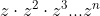(EN) Sabendo que $Número complexo. Png$ , é o número complexo qual o menor inteiro positivo n, para o qual o produto $Número complexo. Png.latex?z%5Ccdot%20z%5E%7B2%7D%5Ccdot%20z%5E%7B3%7D..$ é um real positivo?
a) 1

b) 2

c) 3

d) 4

e) 5

Não consegui desenvolver.

Eduardo Rabelo

26.08.2020 10:04:22

por **Elcioschin** Qua 26 Ago 2020, 10:51

z¹ = cos60º + i.sen60º = 1/2 + i.√3/2
z² = cos120º + i.sen120º = -1/2 + i.√3/2
z³ = cos180º + i.sen180º = -1

z¹.z² = (i.√3/2 + 1/2).(i.√3/2 - 1/2) = (i.√3/2)² - (1/2)² = - 3/4 - 1/4 = -1

z¹.z².z³ = (-1).(-1) = 1

por **Eduardo Rabelo** Qua 26 Ago 2020, 11:03

Elcio, entendi a resolução, mas se fosse um número n muito grande maior que 6, por exemplo. Teria que ir testando um por um, ou há uma maneira de encontrar uma lógica ou algo do tipo?

Eduardo Rabelo

26.08.2020 11:02:17

por **Elcioschin** Qua 26 Ago 2020, 11:21

z¹.z².z³.z⁴. ..... .zⁿ = z^{1+2+3+4+ .... +n}

No expoente temos uma PA com a1 = 1, r = 1, an = n ---> S = n.(n + 1)/2

z^n.(n+1)/2 = cos[60º.n.(n+1)/2] + i.sen[60º.n.(n+1)/]

Para ser real positivo ---> 60º.n.(n + 1)/2 = 360º ---> n² + n - 12 = 0

Raízes n = - 4 e n = 3

por Conteúdo patrocinado

Número complexo.

Número complexo.

Re: Número complexo.

Re: Número complexo.

Re: Número complexo.

Re: Número complexo.

Um fórum livre e democrático.