Lista de questões combinatória
2 participantes
PiR2 :: Questões Especiais :: Olimpíadas :: Matemática
Página 1 de 1
 Lista de questões combinatória
Lista de questões combinatória
Várias pulgas ficam nas casas de um tabuleiro de xadrez 10 x 10 (no máximo um ponto a cada casa). A cada minuto, todas as pulgas saltam simultaneamente para as casas adjacentes. Cada ponto começa a pular em uma das quatro direções (cima, baixo, esquerda, direita) e continua pulando nessa direção enquanto é possível; caso contrário, inverte a direção do contrário. Aconteceu que durante uma hora, duas pulgas nunca ocuparam a mesma casa. Encontre o número máximo possível de pulgas no tabuleiro.
Última edição por Zelderis megantron em Qua 08 Jan 2020, 09:33, editado 1 vez(es)
Barbaducki- Recebeu o sabre de luz

- Mensagens : 119
Data de inscrição : 14/04/2019
Idade : 25
Localização : Rio de Janeiro
 Re: Lista de questões combinatória
Re: Lista de questões combinatória
Em primeiro lugar, é fácil ver que não é possível obter mais do que 40 pulgas porque qualquer linha ou coluna tem no máximo duas pulgas.
Vamos agora encontrar uma construção que atinja 40 pulgas.
Antes de tudo, observe que se a pulga A estiver inicialmente em uma casa branca do tabuleiro de xadrez e a pulga B estiver inicialmente em uma casa preta, as pulgas nunca poderão estar na mesma casa.
Portanto, basta construir um exemplo em que existem 20 pulgas em casas brancas, de modo que nenhuma delas acabe na mesma casa a qualquer momento. De fato, um exemplo de 20 pulgas em casas pretas pode ser obtido analogamente (ou simplesmente refletindo sobre um eixo de simetria), e a combinação desses dois conjuntos de 20 pulgas terminaria o problema.
Então, vamos construir um exemplo de 20 pulgas em casas brancas.
Observe que deve haver exatamente uma pulga em cada linha e coluna; caso contrário, existem duas em alguma linha/coluna; portanto, porque ambos estão em casas brancas, eles coincidirão em algum momento.
Rotule as linhas 0, 1, 2,..., 9 de cima para baixo e as colunas 0, 1, 2,..., 9 da esquerda para a direita.
Para cada 0 ≤ i ≤ 9, deixe r_i indicar o número de minutos depois que as pulgas começam a pular que leva para que a pulga da i-ésima linha alcançar a coluna mais à esquerda (coluna 0 )
Defina c_i da mesma forma que o número de minutos que a pulga leva na i-ésima coluna para alcançar a linha superior (linha 0).
Trabalhando no módulo 18 (dado que o movimento das pulgas é periódico com período 18 ), vemos que a condição da pulga na i-ésima linha que não cruza a pulga na j-ésima coluna é equivalente a:

onde os conjuntos são de classes de resíduos módulo 18.
No entanto, pode-se ver que isso é equivalente a:
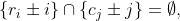
onde os conjuntos são novamente classes de resíduos módulo 18.
A partir daqui, podemos nos concentrar na construção dos conjuntos {r_i ± i} e {c_j ± j}, e chegamos à construção:
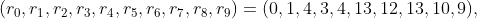
e
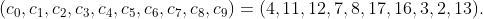
Isso produz a construção anexa, e um argumento análogo para pulgas em casas pretas (ou simplesmente reflexo em um eixo vertical de simetria) obtemos 40 pulgas.
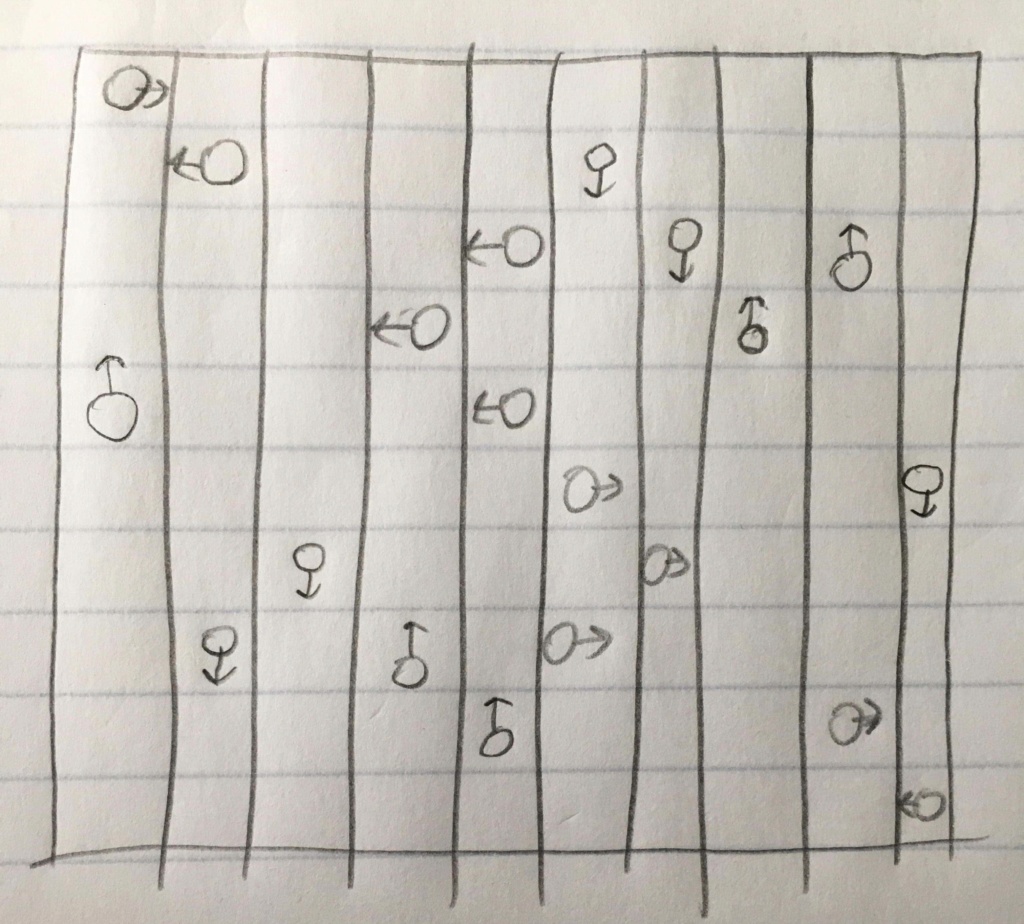
Vamos agora encontrar uma construção que atinja 40 pulgas.
Antes de tudo, observe que se a pulga A estiver inicialmente em uma casa branca do tabuleiro de xadrez e a pulga B estiver inicialmente em uma casa preta, as pulgas nunca poderão estar na mesma casa.
Portanto, basta construir um exemplo em que existem 20 pulgas em casas brancas, de modo que nenhuma delas acabe na mesma casa a qualquer momento. De fato, um exemplo de 20 pulgas em casas pretas pode ser obtido analogamente (ou simplesmente refletindo sobre um eixo de simetria), e a combinação desses dois conjuntos de 20 pulgas terminaria o problema.
Então, vamos construir um exemplo de 20 pulgas em casas brancas.
Observe que deve haver exatamente uma pulga em cada linha e coluna; caso contrário, existem duas em alguma linha/coluna; portanto, porque ambos estão em casas brancas, eles coincidirão em algum momento.
Rotule as linhas 0, 1, 2,..., 9 de cima para baixo e as colunas 0, 1, 2,..., 9 da esquerda para a direita.
Para cada 0 ≤ i ≤ 9, deixe r_i indicar o número de minutos depois que as pulgas começam a pular que leva para que a pulga da i-ésima linha alcançar a coluna mais à esquerda (coluna 0 )
Defina c_i da mesma forma que o número de minutos que a pulga leva na i-ésima coluna para alcançar a linha superior (linha 0).
Trabalhando no módulo 18 (dado que o movimento das pulgas é periódico com período 18 ), vemos que a condição da pulga na i-ésima linha que não cruza a pulga na j-ésima coluna é equivalente a:
onde os conjuntos são de classes de resíduos módulo 18.
No entanto, pode-se ver que isso é equivalente a:
onde os conjuntos são novamente classes de resíduos módulo 18.
A partir daqui, podemos nos concentrar na construção dos conjuntos {r_i ± i} e {c_j ± j}, e chegamos à construção:
e
Isso produz a construção anexa, e um argumento análogo para pulgas em casas pretas (ou simplesmente reflexo em um eixo vertical de simetria) obtemos 40 pulgas.


NikolsLife- Padawan

- Mensagens : 84
Data de inscrição : 10/12/2019
 Tópicos semelhantes
Tópicos semelhantes» Finais - França 2016 (Lista de questões)
» Lista de questões (POTI, lógica II) - Álgebra
» Questões da lista Álgebra básica (Pré cone sul)
» Questões - Combinatória
» questoes de analise combinatoria
» Lista de questões (POTI, lógica II) - Álgebra
» Questões da lista Álgebra básica (Pré cone sul)
» Questões - Combinatória
» questoes de analise combinatoria
PiR2 :: Questões Especiais :: Olimpíadas :: Matemática
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












