Domínio de uma função

por juliagq7 Qui 05 Set 2019, 15:32

Sejam f e g funções de domínio real. Para x ∈ R, define-se h(x)= √f(x) - g(x) (a expressão toda está dentro da raiz quadrada). Obtenha, em cada caso, o domínio da função h, sendo dados os gráficos das funções f e g:

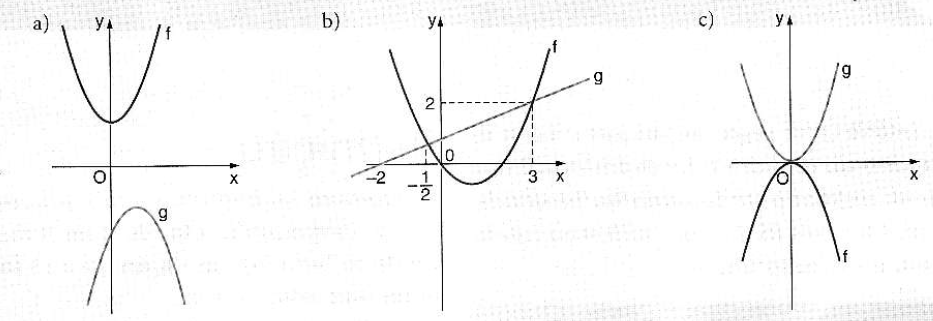
Alguém poderia me ajudar a resolver? Estou tendo algumas dúvidas, mas sei q f(x) tem de ser > g(x) para que não haja raiz quadrada de número negativo e aí a função não ter valor real...

por **Elcioschin** Qui 05 Set 2019, 22:23

a) f(x) > 0 ---> g(x) < 0 ---> - g(x) > 0 ---> f(x) - g(x) > 0 ---> Domínio: ℝ

b) No intervalo [-1/2 , 3] f(x) ≥ g(x) ---> Domínio: - 1/2 ≤ x ≤ 3

c) Para a > 0 ---> f(x) = a.x² ---> g(x) = - a.x²

h(x) = f(x) - g(x) ---> h(x) = a.x² - (- a.x²) ---> h(x) = 2.a.x²

h(x) é uma parábola com a concavidade voltada para cima e raiz dupla x = 0
Esta função h(x) é sempre positiva ou nula ---> Domínio: ℝ

Domínio de uma função

Domínio de uma função

Re: Domínio de uma função

Um fórum livre e democrático.