Escola Naval MHS
4 participantes
PiR2 :: Questões Especiais :: Escolas Militares :: Física
Página 1 de 1
 Escola Naval MHS
Escola Naval MHS
Olá ... meus consagrados. Trago-lhes desfios. Fui incapaz.
Analise o grafico abaixo
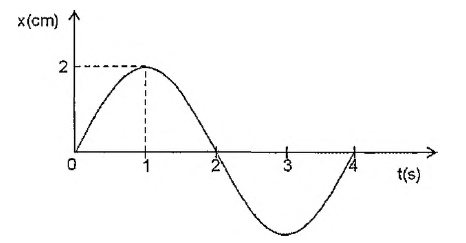
o grafico acima representa a posição x de uma particula que realiza um MHS , em função do tempo t. A equação que relaciona a velocidade v, em cm/s, da particula com sua posição é:

Forte abraço... Não manjo. Quem puder colaborar com a explicação estarei muito grato.
Analise o grafico abaixo

o grafico acima representa a posição x de uma particula que realiza um MHS , em função do tempo t. A equação que relaciona a velocidade v, em cm/s, da particula com sua posição é:

Forte abraço... Não manjo. Quem puder colaborar com a explicação estarei muito grato.
Teodoro97en- Iniciante
- Mensagens : 4
Data de inscrição : 18/02/2019
Idade : 27
Localização : Campo Grande MS
 Re: Escola Naval MHS
Re: Escola Naval MHS
T = 4 s
w = 2.pi/T ---> T é o período
x = 2.cos(w.t - pi/2) ---> x = 2.cos[(2.pi/T).t - θ] ---> x = 2.cos[(2.pi/4).t - pi/2] --->
x = 2.cos[(pi/2).t - pi/2] ---> I
Conferindo
Para t = 0 ---> x(0) = 2.cos(-pi/2) ---> x(0) = 0 ---> OK
Para t = 1 ---> x(1) = 2.cos(0) ---> x(0) = 2 ---> OK
Para t = 2 ---> x(2) = 2.cos(pi/2) ---> x(2) = 0 ---> OK
Para t = 3 ---> x(3) = 2.cos(pi) ---> x(3) = - 2 ---> OK
Para t = 4 ---> x(4) = 2.cos(3.pi/2) ---> x(4) = 0 ---> OK
x² = 4.cos²[(pi/2).t - pi/2] ---> x² = 4.{1 - sen²[(pi/2).t - pi/2]} ---> II
V = - w.A.sen(w.t - pi/2) ---> V = - (pi/2).2.sen[(pi/2).t - pi/2] ---> V = - pi.sen[(pi/2).t - pi/2] --->
V² = pi².sen²[(pi/2).t - pi/2] ---> sen²[(pi/2).t - pi/2] = V²/pi² = III
III em II ---> x² = 4.(1 - V²/pi²) ---> x² = 4 - 4.V²/pi² ---> 4.V²/pi² = 4 - x² ---> V² = pi².(1 - x²/4)
w = 2.pi/T ---> T é o período
x = 2.cos(w.t - pi/2) ---> x = 2.cos[(2.pi/T).t - θ] ---> x = 2.cos[(2.pi/4).t - pi/2] --->
x = 2.cos[(pi/2).t - pi/2] ---> I
Conferindo
Para t = 0 ---> x(0) = 2.cos(-pi/2) ---> x(0) = 0 ---> OK
Para t = 1 ---> x(1) = 2.cos(0) ---> x(0) = 2 ---> OK
Para t = 2 ---> x(2) = 2.cos(pi/2) ---> x(2) = 0 ---> OK
Para t = 3 ---> x(3) = 2.cos(pi) ---> x(3) = - 2 ---> OK
Para t = 4 ---> x(4) = 2.cos(3.pi/2) ---> x(4) = 0 ---> OK
x² = 4.cos²[(pi/2).t - pi/2] ---> x² = 4.{1 - sen²[(pi/2).t - pi/2]} ---> II
V = - w.A.sen(w.t - pi/2) ---> V = - (pi/2).2.sen[(pi/2).t - pi/2] ---> V = - pi.sen[(pi/2).t - pi/2] --->
V² = pi².sen²[(pi/2).t - pi/2] ---> sen²[(pi/2).t - pi/2] = V²/pi² = III
III em II ---> x² = 4.(1 - V²/pi²) ---> x² = 4 - 4.V²/pi² ---> 4.V²/pi² = 4 - x² ---> V² = pi².(1 - x²/4)

Elcioschin- Grande Mestre

- Mensagens : 73164
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Teodoro97en- Iniciante
- Mensagens : 4
Data de inscrição : 18/02/2019
Idade : 27
Localização : Campo Grande MS
 Re: Escola Naval MHS
Re: Escola Naval MHS
Porque todas as alternativas tem V², pi², x²
Eu elevei ao quadrado para chegar na alternativa correta.
Eu elevei ao quadrado para chegar na alternativa correta.

Elcioschin- Grande Mestre

- Mensagens : 73164
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
 Re: Escola Naval MHS
Re: Escola Naval MHS
Mestre, a fase inicial da primeira equação não deveria ser [latex]\frac{3\pi }{2}[/latex] ?Elcioschin escreveu:T = 4 s
w = 2.pi/T ---> T é o período
x = 2.cos(w.t - pi/2) ---> x = 2.cos[(2.pi/T).t - θ] ---> x = 2.cos[(2.pi/4).t - pi/2] --->
x = 2.cos[(pi/2).t - pi/2] ---> I
Conferindo
Para t = 0 ---> x(0) = 2.cos(-pi/2) ---> x(0) = 0 ---> OK
Para t = 1 ---> x(1) = 2.cos(0) ---> x(0) = 2 ---> OK
Para t = 2 ---> x(2) = 2.cos(pi/2) ---> x(2) = 0 ---> OK
Para t = 3 ---> x(3) = 2.cos(pi) ---> x(3) = - 2 ---> OK
Para t = 4 ---> x(4) = 2.cos(3.pi/2) ---> x(4) = 0 ---> OK
x² = 4.cos²[(pi/2).t - pi/2] ---> x² = 4.{1 - sen²[(pi/2).t - pi/2]} ---> II
V = - w.A.sen(w.t - pi/2) ---> V = - (pi/2).2.sen[(pi/2).t - pi/2] ---> V = - pi.sen[(pi/2).t - pi/2] --->
V² = pi².sen²[(pi/2).t - pi/2] ---> sen²[(pi/2).t - pi/2] = V²/pi² = III
III em II ---> x² = 4.(1 - V²/pi²) ---> x² = 4 - 4.V²/pi² ---> 4.V²/pi² = 4 - x² ---> V² = pi².(1 - x²/4)
Vi uma resolução interessante usando [latex]V^{2}= w^{2}(A^{2}-x^{2})[/latex]

Tomaz1- Recebeu o sabre de luz

- Mensagens : 168
Data de inscrição : 12/10/2020
Idade : 21
 Re: Escola Naval MHS
Re: Escola Naval MHS
Note que eu usei a fase inicial pi/2 e testei para vários valores de x e deu certo
Teste o 3.pi/2 na minha fórmula e veja se dá certo. Acredito que não.
Mas note que a minha fórmula é x = 2.cos[(pi/2).t - pi/2]
Talvez dê certo, se você fizer o teste com a fórmula x = 2.cos[(pi/2).t + 3.pi/2]
Teste o 3.pi/2 na minha fórmula e veja se dá certo. Acredito que não.
Mas note que a minha fórmula é x = 2.cos[(pi/2).t - pi/2]
Talvez dê certo, se você fizer o teste com a fórmula x = 2.cos[(pi/2).t + 3.pi/2]

Elcioschin- Grande Mestre

- Mensagens : 73164
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Tomaz1 gosta desta mensagem
 Re: Escola Naval MHS
Re: Escola Naval MHS
I) Aplique Torricelli: v2 = w2.(A2 – x2), onde A = 2cm e w = (2p/T) = (2p/4) = (p/2) rad/s, então: v2 = (p/2)2.(22 – x2) :registered: v2 = p2.[1 – (x2/4)]
Julielly- Iniciante
- Mensagens : 6
Data de inscrição : 12/06/2021
PiR2 :: Questões Especiais :: Escolas Militares :: Física
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












