Super Cálculo

por **gilberto97** Sáb 03 Jun 2017, 23:34

Considero esta a questão mais desafiadora que já imaginei.

Considere a curva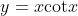 $Super Cálculo Gif$ .

a) Represente-a no plano cartesiano.
b) Calcule a área da figura delimitada pela curva obtida e os eixos x e y, no intervalo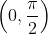 $Super Cálculo Gif$ do eixo x.

Quero deixar claro que na alternativa "a" jogar a equação num site que forneça o gráfico ou no geogebra não é solução!

por **gilberto97** Dom 11 Jun 2017, 19:07

up! :SW1:

por RioBrancoabcRetorna Sáb 22 Jul 2017, 15:48

Desafios cuja resposta eu sei....
Onde está?

por **Willian Honorio** Ter 20 Fev 2018, 22:20

Gostaria de ver a resolução, tentei que só Sad

. O gráfico nem é tão difícil assim, na integral, porém, só chego a igualdades.

por **gilberto97** Ter 20 Fev 2018, 22:37

Boa noite, Willian. Foi bom você ter me lembrado hahaha

De fato, o gráfico é "tranquilo", vou deixar minha resolução para a integral.

Resolvendo a integral:

por **Willian Honorio** Ter 20 Fev 2018, 22:57

Caro Gilberto. Já não consigo enxergar o que fez na primeira linha, na integração por partes.

por **gilberto97** Ter 20 Fev 2018, 22:59

Olá Willian. Chamei x de u e cotxdx de dv.

u = x
du = dx

dv = cotxdx
v = ln(sinx)

int udv = uv - int vdu

uv = xln(sinx) (Fácil ver que se anula nos limites considerados).

por **Willian Honorio** Ter 20 Fev 2018, 23:18

Ah! Entendi. Tuas escolhas certamente foram mais sábias que as minhas, pequei também nessa última linha. Acredito que cometi um erro bastante elementar, devo então considerar o limite das primitivas em determinado ponto no T.F.C? Estava calculando o próprio valor da primitiva em um ponto dado, o que me impedia de calcular x.ln(sinx) pois teríamos ln0 :suspect:.

por **gilberto97** Ter 20 Fev 2018, 23:21

Não entendi muito bem o que você quis dizer, Willian.

por **Willian Honorio** Ter 20 Fev 2018, 23:26

Você disse que x.ln(sinx) se anula nos limites considerados, estava falando disso:

$x.\ln \left (\sin x \right ) |_{0}^{\frac{\pi }{2}}=0$

Eu disse que cometi um erro elementar, pois não sabia que essa diferença era um limite no Teorema Fundamental do Cálculo. Eu interpretava equivocadamente essa diferença.