Problemas sobre circunferência - FME

Escreva a equação da circunferência que tangencia a reta x + 2y - 6 = 0 no ponto de ordenada -1 e determina na circunferência x^2 + y^2 = 4 uma corda paralela ao eixo dos x. 

Gabarito: x^2 + (y+17)^2 = 320 

Não estou conseguindo nem interpretar a questão.

Olá,

Uma consideração inicial: ao se deparar com um exercício desse numa prova ou vestibular, pode pular sem remorso. Pois a resolução demora e gasta muito espaço, fora o risco de você se perder no meio da resolução.. 




1) Primeiro vamos determinar a equação da circunferência que tangencia a reta x +2y - 6 = 0 no ponto de ordenada -1.

Equação reduzida da circunferência de C(x_c,y_c) e raio R:
(x - x_c)^2 + (y - y_c)^2 = R^2

Vou chamar de P(x_p, -1) o ponto de tangência entre a reta e a circunferência.

Pois bem, concorda que a distância do centro C à reta r: x + 2y - 6 = 0 vale R ?

Distância de ponto à reta: d_{c,r} = \frac{|a*x_c + b*y_c + c|}{\sqrt{a^2 + b^2}}
R = \frac{|1*x_c + 2*y_c - 6|}{\sqrt{1^2 + 2^2}}
R = \frac{|x_c + 2*y_c - 6|}{\sqrt{5}}

No entanto, a distância de C(x_c, y_c) ao ponto P (x_p, -1) também é igual a R (pois P pertence à circunferência):
d_{c,p} = R
d_{c,p} = \frac{|x_c + 2*y_c - 6|}{\sqrt{5}}
\sqrt{(x_c - x_p)^2 + (y_c -(-1))^2} = \frac{|x_c + 2*y_c - 6|}{\sqrt{5}}  
\sqrt{(x_c - x_p)^2 + (y_c + 1)^2} = \frac{|x_c + 2*y_c - 6|}{\sqrt{5}}
\sqrt{5[(x_c - x_p)^2 + (y_c + 1)^2]} = |x_c + 2*y_c - 6| (I)


2) A circunferência desejada determina na circunferência x^2 + y^2 = 4 uma corda paralela ao eixo dos x.


De cara, concluímos que as circunferências são secantes entre si. Assim, vão haver 2 pontos que pertencem às duas circunferências. Vou chamar esses pontos de intersecção de A(x_a, y_a) e B(x_b, y_a) . (Os dois pontos tem o mesmo y pois pertencem à uma reta paralela ao eixo x).
...

Vou parar por aqui, tá ficando difícil fazer direto em latex e sem auxílio de um desenho..
A ideia para exercicios assim é continuar explorando as informações fornecidas a fim de achar relações entre as incógnitas que foram estabelecidas (x_p, x_c, x_a, y_a ...) , e quando tiver o suficiente você monta o sistema (mais aconselhável) ou vai fazendo substituições para encontrar o valor de cada uma..

Dica: é sempre muito facilitador você fazer um desenho bom e grande, fica mais tranquilo de entender e as vezes existe uma sacadinha de geometria plana ou de uso de vetores que torna a resolução bem mais simples.



Abraço!

Muito obrigado, ótima resolução!

Mas só uma dúvida, essa corda que uma circunferência determina na outra, eu aproximaria para uma reta? Não consegui entender isso. 

 Esse é o tipo de questão que a gente deixa pro concorrente fazer haha  
As últimas questoes dos capítulos do FME são sempre assim, questão de braço :/

Então, a corda que ele se refere é a reta determinada pelos dois pontos de intersecção.
Representei-a neste desenho, em vermelho.


Sim, para questões de Geometria Analítica, Análise Combinatória e Geometria Espacial sem desenho no enunciado o mais recomendável na maioria das vezes é pular/deixar por último.


Abraço.

Olhando agora, tem um conceito de geometria plana que pode facilitar as coisas.

É intuitivo demonstrar que se você traçar uma reta que liga os dois centros, ela intercepta a corda vermelha perpendicularmente, portanto vai seccionar a corda em 2 partes iguais (ou seja, vai cortar a corda bem no ponto médio)
Acho que a resolução sai mais rápido se você explorar isso.
Usando as coordenadas dos pontos de intersecção para montar a equação da reta que contém a corda e mexer com os coeficientes angulares da reta da corda (m) com a reta que liga os centros (-1/m), é uma ideia..

No mais, exercício bem exigente. Fiz um discursivo do ITA parecido com esse e foi bem mais tranquilo..


Abraço.

Esse FME é do iezzi, né? Que questão!

Quem sabe uma figura (sem escala) ajuda: 

Eu sei que a questão está na parte do ensino médio, mas caso você saiba cálculo isso ajuda bastante (e caso alguém saiba e se perguntou se tem como resolver usando cálculo, tem sim). 

Primeiro, vamos organizar algumas informações:



Assim, o ponto A de tangência entre a reta e a circunferência A é  

Temos também a circunferência B  

Se as circunferências formam uma corda na intersecção, então elas são secantes; se essa corda é paralela ao eixo x, os pontos de secância são da forma e . Usando a fórmula da circunferência B provamos que .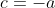 





Então,  e como as circunferência são secantes e não tangentes: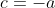  

A circunferência A tem fórmula  

Utilizando os pontos S e P, vem que:  e , o que implica que 

Agora é que entra o cálculo: derivamos implicitamente a equação da circunferência A.









Voltando agora a reta tangente no ponto , temos que seu coeficiente angular é 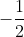, de acordo com a equação  

Assim: 



E portanto: 



E assim a equação da circunferência C está quase pronta:
 


Utilizando o ponto A mais uma vez: 




E por fim:

Espero que alguma etapa da minha resolução possa ajudar alguém a resolver a questão sem cálculo, e se eu conseguir postarei também.

Samuel, ótima resolução.
É mesmo fascinante a eficácia e sofisticação do Cálculo.

Esdras,
O FME é do Iezzi sim, majoritáriamente digamos. Mas o volume de análise combinatória do FME, por exemplo, parece ter sido feito só por uma pessoa (Samuel Hazzan), enquanto outros volumes são do Iezzi ou sozinho ou com outros matemáticos. Que questão, mesmo!

JOAOCASSIANO,
Veja como fica bem mais elucidativo com o gráfico do Elcioschin, mas imagine agora se dá para fazer um esboço desses e resolver o exercício em uns 5 minutos (que é mais ou a menos a média do tempo por questão de matemática no vestibular)...


Abraços!

Pietro

Não dá tempo. E você mesmo disse isto na sua 1ª mensagem.
Se eu estivesse fazendo a prova, deixaria esta questão de lado e partiria para aquelas mais simples e imediatas.
Depois, caso sobrasse algum tempo, eu voltaria a ela, mesmo que não conseguisse terminar:

Faria um esboço do gráfico, montaria as equações e indicaria o passo-a-passo do caminho a ser seguido.
Por ser uma questão discursiva, a banca, vendo tudo isto, tende a dar, pelo menos, uma nota parcial.