(UNIRIO) MCU

por stefanyscastro Dom 20 Mar 2016, 12:04

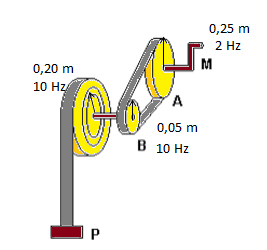
O mecanismo apresentado na figura anterior é utilizado para enrolar mangueiras após terem sido usadas no combate a incêndios. A mangueira é enrolada sobre si mesma, camada sobre camada, formando um carretel cada vez mais espesso.
(UNIRIO) MCU 25i52z8

O diâmetro da polia A é igual a 50 cm e o diâmetro da polia B é igual a 10cm. A manivela é girada com movimento uniforme realizando cento e vinte rotações por minuto. Adotando (UNIRIO) MCU V7W1tampqW5ubmFhYVRUVEZGRgAAAAAAAAAAAAAAAAAAAAAAACH5BAEAAAAALAAAAAAoAAwAAARaEMhJq700qK2MwGBoKcOUHGIaKtSmviKCAppy2BwsDsqnDQUW68IpGok2gkQRAPScutTgcPhINM1hNDQ4TQRD7RbkWlrFLaO6Uu7OoMvxqACYVidatLzWsUYAADsAAAAAAAAAAAA=

(UNIRIO) MCU V7W1tampqW5ubmFhYVRUVEZGRgAAAAAAAAAAAAAAAAAAAAAAACH5BAEAAAAALAAAAAAoAAwAAARaEMhJq700qK2MwGBoKcOUHGIaKtSmviKCAppy2BwsDsqnDQUW68IpGok2gkQRAPScutTgcPhINM1hNDQ4TQRD7RbkWlrFLaO6Uu7OoMvxqACYVidatLzWsUYAADsAAAAAAAAAAAA=

, julgue os item a seguir.
(1) Se a polia em que a mangueira é enrolada possui diâmetro igual a 40cm e a mangueira possui 50m de comprimento e 4,0cm de espessura, podemos afirmar que, se a mangueira se encontra completamnete desenrolada, os bombeiros gastarão menos de 2,0s para enrolá-la.

Spoiler:

por **Christian M. Martins** Dom 20 Mar 2016, 15:19

Vamos "quebrar" a circunferência da polia e dispor-la como uma reta. Repare que na primeira volta (quando a mangueira está percorrendo apenas a circunferência da polia, sem ter começado a enrolar-se em si mesmo), ela se enrola do seguinte comprimento, sendo D o diâmetro:

2π(D/2) = πD = 120 cm

Quando ela começa a dar uma volta sobre si mesma (na segunda volta) então, tem-se que o comprimento enrolado é:

2π((D + 4)/2) = π(D + 8) = 144 cm

Na terceira volta:

2π((D + 8)/2) = π(D + 16) = 168 cm

Repare que o comprimento a ser enrolado por revolução é dado por uma P.A. cuja razão é 24 cm. Assim:

S_n = n(a₁ + a_n)/2 = n(120 + a_n)/2

Deseja-se que S_n = 5000 cm:

5000 = n(120 + a_n)/2 ---> 10000 = n(120 + a_n) ---> n = 10000/(120 + a_n) (I)

Mas:

a_n = a₁ + (n - 1)r ---> a_n = 120 + (n - 1)24 = 120 + 24n - 24 = 24n + 96 (II)

Fazendo:

(I) em (II): n = 10000/(120 + 24n + 96) = 10000/(24n + 216) ---> 24n² + 216n - 10000 = 0

Resolvendo, obtém-se n ≈ 16,4 revoluções.

A velocidade escalar da polia A é igual à velocidade escalar da polia B:

V_a = V_b
V_a = ω_ar_a
ω_a = 120*(2π)/60 = 2*(2π) = 4π = 12 rad/s
V_a = V_b = 12*r_a = 12*0,25 = 3 m/s

A velocidade angular da polia B é igual à velocidade angular da polia da mangueira:

V_b = ω_br_b ---> ω_b = V_b/r_b = 3/0,05 = 60 rad/s

Então o tempo a ser percorrido do início do enrolar ao fim será:

16,4*2π/(60) = 1,64 s

por **Euclides** Dom 20 Mar 2016, 22:25

Na PA (inteligentemente procurada) parece que você andou misturando diâmetros e raios.

$\\R_0=0,20\;m\;\;\;\to\;\;\;2\pi R_0=1,2\;m\\R_1=0,24\;m\;\;\;\to\;\;\;2\pi R_1=1,44\;m\\R_2=0,28\;m\;\;\;\to\;\;\;2\pi R_2=1,68\;m\\\\\text{a raz\~ao da PA \'e: }r=0,24\\\\50=\frac{1,2+1,2+(n-1)0,24}{2}\cdot n\;\to\;n=16,4\;\;\text{rev}$

(UNIRIO) MCU Im1