Colisão Bidimensional
3 participantes
PiR2 :: Física :: Mecânica Geral
Página 1 de 1
 Colisão Bidimensional
Colisão Bidimensional
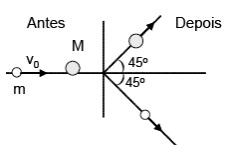
Um corpo de massa m e velocidade v0 colide com um segundo corpo de massa M=3m, inicialmente em repouso. Depois da colisão, a velocidade de cada corpo forma um ângulo de 45° com a direção da velocidade inicial. Nessas condições, a razão entre a energia cinética final e a energia cinética inicial é igual a:
A) 1/3
B) 1/2
C) 5/9
D) 2/3
E) 3/4
Após a colisão podemos decompor as velocidades finais dos corpos de massas M e m. Desse modo, no eixo x os corpos de massa M e m possuem as respectivas quantidades de movimento, M.vf.cos 45° e m.vf.cos 45°. daí, temos:
Em x:
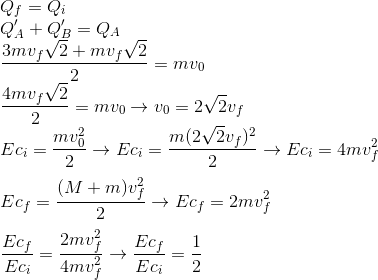
O que eu errei?

A) 1/3
B) 1/2
C) 5/9
D) 2/3
E) 3/4
Após a colisão podemos decompor as velocidades finais dos corpos de massas M e m. Desse modo, no eixo x os corpos de massa M e m possuem as respectivas quantidades de movimento, M.vf.cos 45° e m.vf.cos 45°. daí, temos:
Em x:
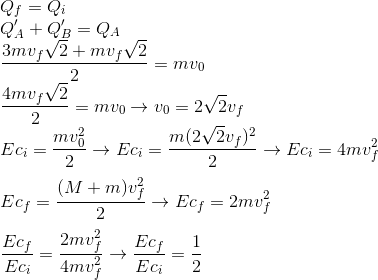
O que eu errei?
Convidado- Convidado
 Re: Colisão Bidimensional
Re: Colisão Bidimensional
As velocidades finais de ambas NÃO são iguais: Considere que m tenha velocidade v'f e M = 3.m tenha v"f
Para saber a relação entre elas faça a equação de equilíbrio no eixo y:
m.v'f,sen45º = 3.m.v"f.sen45º ---> v'f = 3.v"f
Faça agora equação da quantidade de movimento no eixo x, calcule v'f e v"f e calcule as energias cinéticas.
Para saber a relação entre elas faça a equação de equilíbrio no eixo y:
m.v'f,sen45º = 3.m.v"f.sen45º ---> v'f = 3.v"f
Faça agora equação da quantidade de movimento no eixo x, calcule v'f e v"f e calcule as energias cinéticas.

Elcioschin- Grande Mestre

- Mensagens : 73172
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
 Re: Colisão Bidimensional
Re: Colisão Bidimensional
O cálculo da energia se dá só com as velocidades do eixo x? não entendi o que foi feito

Raquel Valadão- Mestre Jedi

- Mensagens : 523
Data de inscrição : 04/04/2017
Localização : Bahia
 Re: Colisão Bidimensional
Re: Colisão Bidimensional
Não, para verificar a razão entre as energias é preciso estabelecer a relação entre as velocidades das partículas depois da colisão e em seguida relacioná-las com a velocidade vo.
Seja a partícula 1 de massa = m e velocidade v1 após a colisão;
Seja a partícula 2 de massa = 3.m e velocidade v2 após a colisão;
I) A quantidade de movimento inicial é apenas no eixo x e irá se conservar:
Qi = Qf
II) A condição (I) implica iguais quantidades de movimento da partícula 1 e da partícula 2 no eixo y após a colisão:
Q1y = Q2y
m.v1 = 3m.v2
v1 = 3.v2
III) No eixo x a soma das quantidades de movimento é igual a Qi:
Qi = Q1x + Q2x
m.vo = m.v1.(√2/2) + 3m.(v1/3).(√2/2)
vo = (√2.v1)/2 + (√2.v1/2)
vo = √2.v1
IV) Sabendo a relação entre v1 = 3.v2 e vo = √2.v1 podemos calcular as energias em função de vo ou v1 e a razão solicitada:
Eci = m.(√2.v1)²/2
Ecf = m.v1²/2 + 3.m.(v1/3)²/2
Ecf/Eci = 5/9
Seja a partícula 1 de massa = m e velocidade v1 após a colisão;
Seja a partícula 2 de massa = 3.m e velocidade v2 após a colisão;
I) A quantidade de movimento inicial é apenas no eixo x e irá se conservar:
Qi = Qf
II) A condição (I) implica iguais quantidades de movimento da partícula 1 e da partícula 2 no eixo y após a colisão:
Q1y = Q2y
m.v1 = 3m.v2
v1 = 3.v2
III) No eixo x a soma das quantidades de movimento é igual a Qi:
Qi = Q1x + Q2x
m.vo = m.v1.(√2/2) + 3m.(v1/3).(√2/2)
vo = (√2.v1)/2 + (√2.v1/2)
vo = √2.v1
IV) Sabendo a relação entre v1 = 3.v2 e vo = √2.v1 podemos calcular as energias em função de vo ou v1 e a razão solicitada:
Eci = m.(√2.v1)²/2
Ecf = m.v1²/2 + 3.m.(v1/3)²/2
Ecf/Eci = 5/9
Rory Gilmore- Monitor

- Mensagens : 1878
Data de inscrição : 28/05/2019
Localização : Yale University - New Haven, Connecticut
 Tópicos semelhantes
Tópicos semelhantes» Colisão Bidimensional
» Colisão Bidimensional
» Colisão Bidimensional
» Colisão bidimensional
» Colisão Elástica Bidimensional sem ângulos
» Colisão Bidimensional
» Colisão Bidimensional
» Colisão bidimensional
» Colisão Elástica Bidimensional sem ângulos
PiR2 :: Física :: Mecânica Geral
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












