Fuvest - Circunferência
4 participantes
Página 1 de 1
Fuvest - Circunferência
por GutoAz Qui 01 Out 2015, 09:57
No plano cartesiano, os pontos (0, 3) e (−1, 0) pertencem à circunferência C. Uma outra circunferência, de centro em (−1/2, 4) , é tangente a C no ponto (0, 3). Então, o raio de C vale:
gabarito: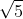
Eu tentei de inúmeras formas e quase nada deu certo. Cheguei ao resultado mas não consegui justificar os cálculos. Gostaria de uma resolução o mais simples possível.
gabarito:
Eu tentei de inúmeras formas e quase nada deu certo. Cheguei ao resultado mas não consegui justificar os cálculos. Gostaria de uma resolução o mais simples possível.
GutoAz- Padawan
- Mensagens : 64
Data de inscrição : 18/03/2015
Idade : 30
Localização : Brasil
Re: Fuvest - Circunferência
por Nina Luizet Qui 01 Out 2015, 13:08
Boa tarde, GutoAz
P = (0,3) e C = (-1/2,4)
m = y-y'/x-x' = 4-3/-1/2-0
m = -2
y-y' = m.(x-x')
y -3 = -2.x
y = -2x+3, na forma (x,-2x+3), sendo equidistante dos pontos (0,3) e (-1,0) que pertencem a circunferência C. Logo,:
V(x-xp')2 + (y-yp')2 = V(x-xp'')2 + (y-yp'')2
V x2 + (-2x+3-3)2 = V(x+1)2 + (-2x+3-0)2 ∴ 1
Sendo assim, O= (1,1) e o raio é igual a distância entre (0,3) e (1,1)
V(1-0)2+ (1-3)2 ∴ V5
P = (0,3) e C = (-1/2,4)
m = y-y'/x-x' = 4-3/-1/2-0
m = -2
y-y' = m.(x-x')
y -3 = -2.x
y = -2x+3, na forma (x,-2x+3), sendo equidistante dos pontos (0,3) e (-1,0) que pertencem a circunferência C. Logo,:
V(x-xp')2 + (y-yp')2 = V(x-xp'')2 + (y-yp'')2
V x2 + (-2x+3-3)2 = V(x+1)2 + (-2x+3-0)2 ∴ 1
Sendo assim, O= (1,1) e o raio é igual a distância entre (0,3) e (1,1)
V(1-0)2+ (1-3)2 ∴ V5
Nina Luizet- matadora
- Mensagens : 1215
Data de inscrição : 21/06/2014
Idade : 25
Localização : Brasil, RN , Mossoró
GutoAz- Padawan
- Mensagens : 64
Data de inscrição : 18/03/2015
Idade : 30
Localização : Brasil
Re: Fuvest - Circunferência
por Ceruko Seg 10 maio 2021, 18:38
Alguém pode me dizer por que o y do centro O é -2x+3?
Ceruko- Estrela Dourada
- Mensagens : 1326
Data de inscrição : 01/07/2020
Idade : 23
Localização : Ribeirão Preto
Re: Fuvest - Circunferência
por Medeiros Seg 10 maio 2021, 22:11
porque o centro O da circunferência C fica sobre a reta y = -2x + 3; e qualquer ponto (x, y) desta reta pode ser escrito como (x, -2x+3).
e por que fica nessa reta? porque os centros de duas circunferências tangentes sempre estão alinhados com o ponto de tangência.
e por que fica nessa reta? porque os centros de duas circunferências tangentes sempre estão alinhados com o ponto de tangência.
Medeiros- Grupo
Velhos amigos do Fórum
- Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
Re: Fuvest - Circunferência
por Ceruko Seg 10 maio 2021, 22:22
Ahh, não sabia dessa, que qualquer ponto era viável.
Obrigado, grande tutor Medeiros!
Obrigado, grande tutor Medeiros!
Ceruko- Estrela Dourada
- Mensagens : 1326
Data de inscrição : 01/07/2020
Idade : 23
Localização : Ribeirão Preto
Medeiros- Grupo
Velhos amigos do Fórum - Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
Ceruko gosta desta mensagem
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
