Problemas Selecionados I

O valor mínimo de 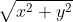 se 5x+12y=60 é igual a:

A)60/13
B)13/5
C)13/12
D)1
E)0

5x + 12y = 60 >>>>>> x = 60 - 12y/5    


[(60 - 12y)/5 ]² + y² = k

3600 - 1440y + 144y²/25 + y² = k
3600 - 1440y + 144y² + 25y²/25 = k
169y² - 1440y + 3600/25 = k

como a concavidade da parábola é para cima em virtude do sinal do coeficiente 'a' , o cálculo do valor minimo para y será : -b/2a
-b/2a
- (-1440)/25 / 2.169/25
1440/2.169
720/169 

5x + 12.720/169 = 60
5x = 60 - 8640/169
x = 60 - 8640/169 / 5

x = 60.169 - 8640/169 / 5
x = 1500/169 / 5
x = 1500/169.5
x = 300/169

V 300²/169² + 720²/169² = k

V300² + 720²/169² = k

V608400/169² = k

780/169 = k

60/13 = k

(Dúvida:De onde tirou essa questão?)

Problemas Selecionados de Matemática, do autor Antônio Luiz Santos, mais conhecido como Gandhi. No mais, obrigado pela resolução. Abraço!