POLÍGONOS REGULARES

"Um polígono diz-se regular se tiver todos os seus lados e ângulos iguais, sejam eles internos ou externos. Todo polígono regular pode ser inscrito em uma circunferência."

Como consequência, todos os quadrados, pentágonos, etc, são semelhantes entre si. Todos os polígonos regulares de 48 lados (ou qualquer número de lados) serão semelhantes entre si.

Não imagino que possam haver 5 polígonos regulares de 48 lados não semelhantes entre si.

No livro do Morgado diz que são 8 polígonos

então ele, em que pese ser "o Morgado", deve dizer -- mostrar ou descrever -- quais são esses polígonos e porquê. Senão, como diz meu filho, até papagaio fala.

Medeiros escreveu:então ele, em que pese ser "o Morgado", deve dizer -- mostrar ou descrever -- quais são esses polígonos e porquê. Senão, como diz meu filho, até papagaio fala.

Entendo, mas essa questão é do livro Geometria II e lá só tem mesmo o gabarito. Não vi nenhuma explicação para isso. Realmente!!!!

Medeiros

Pesquisando descobri que aqui entra o conceito de polígonos estrelados regulares.
Polígono estrelado regular é o polígono estrelado onde todos os lados são congruentes e também todos os ângulos internos são congruentes.

Sejam n e k números naturais tais 4 < n,  1 < k < n-1 e com mdc(n,k)=1 .
Chamamos de polígono estrelado n / k o polígono complexo de n lados obtido a partir da divisão de uma circunferência em n partes congruentes, ligando-se sucessivamente os pontos de divisão de k em k. 
Ou seja, só conseguimos obter um polígono regular quando pulamos para um número que seja primo com n Ex: Se n = 8 teremos polígonos regulares quando pulamos para o 1, 3, 5 e 7. Ainda assim obtemos polígonos repetidos duas vezes. Portanto, a quantidade de polígonos regulares de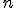  lados é igual à metade da quantidade de números positivos primos com .

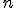Para calcular a quantidade de números primos com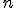  utilizamos a função Totiente de Euler .

O valor  nos dá a quantidade de números primos com 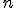 que são menores que .

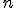Essa função tem as seguintes propriedades:

1)  se 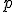 é primo;

2)  se 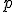 é primo;

3) ,  e 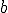 primos entre sí e .


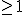Em geral, temos Ø(n)/2 polígonos regulares com n vértices (onde Ø é a função de Euler)


Para n = 48
Ø(48) = Ø(3.16)
Como 3 e 16 são primos entre sí, podemos aplicar a regra 3:
Ø(48)=Ø(3.16)=Ø(3).Ø(2⁴)=(3-1).2^(4-1).(2-1)=2.8.1=16
Portanto temos que a quantidade de polígonos regulares com 48 lados é 
16/2 = 8

(Colaboração: Prof. Caju)

Petras,

obrigado pela pesquisa e esclarecimento.
Então, se pretende-se considerar também os polígonos estrelados, com 48 vértices temos 1 polígono convexo e 7 polígonos estrelados.

Porém quando se fala em polígonos esta-se referindo apenas aos convexos; exemplo: quando se fala em pentágono regular ninguém supõe um pentágono estrelado regular. Assim, se a questão desejava incluir também os estrelados deveria cita-lo explicitamente. Mas acho que aconteceu o seguinte: o livro vinha tratando dos polígonos estrelados e lançou aquela pergunta; então ficou implícito (no livro) ao que a questão se referia. No entanto, a pergunta solta, tal como apresentada neste fórum, fica sem sentido -- daí a correta resposta do Euclides (i.m.)

Quanto a essa explicação do porf. Caju que você trouxe, acho-a muito complicada para a minha cabeça de algebrista pobre. Prefiro assim:

a quantidade de números primos com n, e menores do que n, é dado pelo nº de Euler p_n:

o nº de polígonos diferentes com n lados é dado por   [latex]\frac{p_n}{2}[/latex]

sendo que 1 deles é o polígono convexo (primo 1) e  [latex]\frac{p_n}{2} - 1[/latex] é o número de polígonos estrelados.

___________________________________________________________

então para 48 vértices temos:

48 = 2⁴.3

p₄₈ = 48.(1 - 1/2).(1 - 1/3) = 48.(1/2).(2/3) = 48/3 = 16

p₄₈/2 = 8 polígonos, sendo 1 convexo e 7 estrelados.

Medeiros, de algebrista pobre você não tem nada...realmente é um assunto raramente visto e seria de bom tom mencionar a questão dos polígonos estrelados.....só vi uma questão desse tipo que caiu na escola naval em 1973 "Quantas espécies distintas de polígonos regulares de 100 lados existem?

ah, mas para essa pergunta da Escola Naval em 1973, a resposta é simples: duas espécies, convexo e estrelado -- só isto.

faz um mês que fiz um comentário sobre isto aqui no fórum: https://pir2.forumeiros.com/t177264-matematica-basica#617677