Área de figuras planas

Resolvendo por GA, considerando sistema xOy com vértice inferior esquerdo do quadrado na origem:

A(0, 0), B(0, a), C(a, a), D(a, 0), E(3a/2, a.√3/2), F(2a, 0)
G = cruzamento das retas BF e CD
H = cruzamento das retas BF e DE

Equação da reta BF ---> m = -AB/AF ---> m = - a/2a ---> m = - 1/2 ---> y - a = -(1/2).(x - 0) ---> y = - x/2 + a

Para xD = a ---> yD = -xD/2 + a ---> yD = - a/2 + a ---> yD = a/2 ---> D(a, a/2)

Equação da reta DF ---> m' = tg60º ---> m' = √3 ---> y - 0 =  √3.(x - a) ---> y =  √3.x - (√3- 1).a


Ponto H ----> - xH/2 + a = √3.x - (√3 - 1).a ----> xH = 2.(√3 + 1).a/(√3 + 1) ----> Falta racionalizar e calcular yH


Com as coordenadas de D, G, H basta calcular a área do triângulo ----> S = DG.(xH - xD)/2

Consideramos a reta que corta o retângulo e o triângulo.


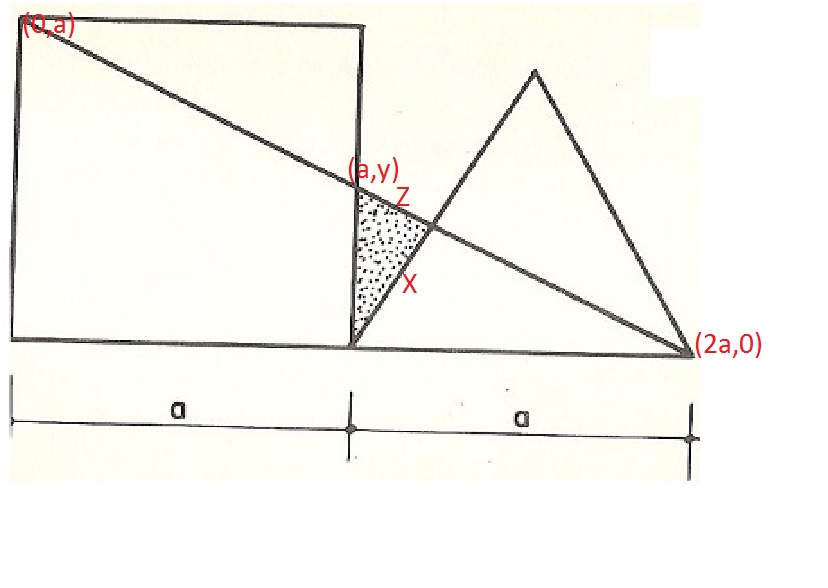
Teremos no quadrado o ponto de onde ela parte: (0,a)
O ponto no triângulo onde ela chega é (2a,0)

Isso nos dá uma reta de equação y = (2a - x)/2

No ponto onde ela corta o quadrado, é (a,y)

Substituindo, descobrimos que y = a/2

Por semelhança de triângulos, descobrimos que X = a√5/5

Agora no triângulo achurado temos 2 lados, a/2 e a√5/5.

Só nos resta saber o tamanho Z, por pitágoras.

a²/4 = 5a²/25 + z²

z = a√20/20

Agora a área do triângulo

a√20/20.a√5/5.1/2

Portanto,  a área hachurada tem valor igual a : a²/20

Creio ser isso

Não entendi nada... 

https://pir2.forumeiros.com/t33966-abcd-e-um-quadrado-e-o-cef-e-equilatero.
Aproveitando essa resol. a área pedida pode ser calculada por:

S= 1/2 . x . a/2 . sen 30º

Isso mesmo como raimundo pereira disse:

S=a²(2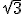-1) /44

Boa tarde para todos!

Vou colocar o resultado que encontrei, apenas a título informativo, para que se possa, depois, comparar os resultados:

S = 0,056002 a²

Não poderei colocar os cálculos que fiz, por ter-me utilizado de tabelas trigonométricas e, no final, a fórmula de Herón.

Retifiquei a parte a√a para a², que é o correto.

Este meu cálculo (após a retificação supra) bate com o gabarito que o amigo Raimundo informou:
S = a²(2√3 - 1)/44 
S = a²(2*1,7320508 - 1)/44 = a²(2,4641016)/44 = a²(0,56002...)





Um bom domingo para todos!

Prezado Ivomilton,
sua resposta não pode ser uma área.
Área tem dimensão 2. Sua resposta a√a tem dimensão 3/2 (menor que 2).

Complementando:
Esse problema é o de nr. 980 do livro Fundamentos de Matemática Elementar Vol 9 de Oswaldo Dolce e Nicolau Pompeo.
O gabarito é a².(2V3-1)/44.

att

Eu retirei a questão do livro Geometria II do Augusto César Morgado, Eduardo Wagner e Miguel Jorge. Pág 170 exercício 269
Não tem resposta, mas pesquisei e é isso mesmo

S=a²(2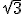-1) /44