Provas "por absurdo"
3 participantes
PiR2 :: Recursos extras :: Demonstrações
Página 1 de 1
 Provas "por absurdo"
Provas "por absurdo"
Olá 
Neste tópico, vou expor algumas demonstrações feitas “por absurdo”, que foi uma das primeiras maneiras que eu aprendi a fazer demonstrações esse ano na faculdade. Além de objetivar o conhecimento da técnica, aos que gostariam de estudar matemática no futuro, vejamos um pouco mais da matemática "rigorosa" que será apresentada nos cursos, em geral.
Para os que não conhecem esta técnica (que tem ideia muito simples), ela consiste no seguinte: Suponhamos que temos uma proposição P1 que queremos provar ser verdadeira. Então supomos, por absurdo, que P1 seja falsa e chegar a um absurdo, ou seja, algo como 1=0 ou em alguma coisa que já sabemos que não é verdade. Claramente não é tudo que pode ser demonstrado por absurdo, devemos tomar cuidado para aplicar essa técnica para mostrarmos fatos que são ou não verdadeiros, e que a sua não falsidade implica que este é verdadeiro.
Certo, agora pode parecer um pouco confuso, mas vou mostrar alguns fatos básicos (e outros nem tanto) utilizando esta técnica e ficará mais claro. Vale ressaltar que demonstrações “por absurdo” ou “por contradição” são especialmente úteis quando queremos provar alguma coisa básica sem com que tenhamos muitas ferramentas ainda.
Vale a pena, para o total entendimento do tópico, a introdução de algumas definições e axiomas que, geralmente, não são conhecidos por alunos de ensino médio, mas que serão facilmente entendidos.
Os axiomas de Peano:
Seja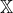 um conjunto e
um conjunto e 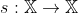 uma função tais que:
uma função tais que:
P1) A função s é injetiva. Ou seja, se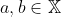 são tais que
são tais que =s(b)) , então
, então 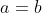
P2)) é um conjunto unitário, onde
é um conjunto unitário, onde ) denota o conjunto imagem de
denota o conjunto imagem de 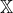 . Diremos que
. Diremos que =\{\textbf{1}\})
P3) (Princípio de Indução) Se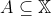 é tal que
é tal que
a)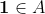
b)&space;\in&space;A)
então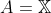
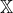 com essas características é dito um conjunto de números naturais e s é sua função sucessor.
com essas características é dito um conjunto de números naturais e s é sua função sucessor.
Bom, mostrar a existência de um conjunto que satisfaz essas características é um pouco mais difícil. Então vamos supor conhecido nosso conjunto de números naturais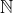 , cujo menor elemento eu defini sendo 1.
, cujo menor elemento eu defini sendo 1.
Números primos: Dizemos que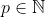 é um número primo quando
é um número primo quando 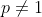 e
e  possui apenas dois divisores:
possui apenas dois divisores:  e ele mesmo.
e ele mesmo.
Menor elemento: Seja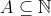 e
e 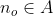 . Dizemos que
. Dizemos que 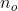 é o menor elemento (ou elemento mínimo) de
é o menor elemento (ou elemento mínimo) de 
quando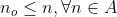
Então vejamos algumas provas.
1. (Princípio da Boa Ordem) Todo subconjunto não vazio de números naturais tem um menor elemento.
• Prova: Seja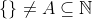 . Se
. Se 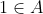 ,
,  é o menor elemento de
é o menor elemento de  e não há o que provar.
e não há o que provar.
Se não, considere o conjunto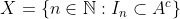 , onde
, onde 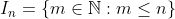 .
. 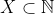 , mas
, mas 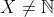 pois
pois 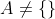 e, então, Princípio de Indução , existe
e, então, Princípio de Indução , existe 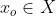 tal que
tal que &space;\not&space;\in&space;X) . Afirmamos que
. Afirmamos que ) (que vamos escrever, da forma convencional, como
(que vamos escrever, da forma convencional, como 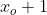 ) é o menor elemento de
) é o menor elemento de  :
:
Com efeito, supondo, por absurdo, que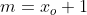 não seja o menor elemento de
não seja o menor elemento de  , existe, então,
, existe, então, 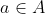 tal que
tal que 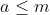 . Contradição, pois
. Contradição, pois 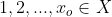 e
e 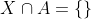 . Portanto
. Portanto  tem um menor elemento.
tem um menor elemento.
Então, segue que qualquer subconjunto não vazio de números naturais tem um menor elemento.
Bom, pode parecer que esse é um Teorema um pouco bobo, mas ele é bem útil visto que vamos usá-lo para provar, utilizando a técnica acima, o princípio de indução de uma forma mais parecido com a que conhecemos!
Definição: Dizemos que um subconjunto ordenado de números naturais satisfaz o Princípio da Boa Ordem se todos os seus subconjuntos têm um menor elemento.
2. O 2º Princípio de Indução: Seja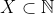 ordenado (e não vazio) com a seguinte propriedade: Dado
ordenado (e não vazio) com a seguinte propriedade: Dado 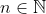 , se
, se  contém todos os números naturais m tais que
contém todos os números naturais m tais que 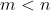 , então
, então 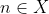 . Nestas condições,
. Nestas condições, 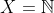
• Prova: Suponhamos, por absurdo, que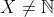 . Então,
. Então, 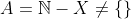 e, pelo Princípio da Boa Ordem,
e, pelo Princípio da Boa Ordem,  tem um menor elemento
tem um menor elemento 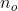 . Daí, segue que que
. Daí, segue que que 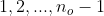 pertencem à
pertencem à  e, por hipótese,
e, por hipótese, 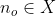 . Absurdo, pois
. Absurdo, pois 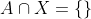 .
.
Portanto,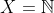
Bom, acredito que, agora, a ideia tenha ficado mais clara. Então vejamos mais algumas provas envolvendo outros temas. Esta é um clássico, provavelmente muitos já viram:
3. A irracionalidade de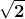 :
:  é irracional
é irracional
Definição(1): Chamamos de raiz quadrada de um número real x, e denotamos por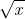 , o único número real tal que
, o único número real tal que 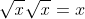
Definição(2): Dizemos que um número real é racional quando existem
é racional quando existem 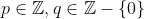 primos entre si tais que
primos entre si tais que 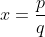 . Caso contrário, dizemos que
. Caso contrário, dizemos que  é irracional.
é irracional.
• Prova: Suponhamos, por absurdo, que seja racional. Isto é, existem
seja racional. Isto é, existem 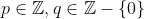 primos entre si tais que
primos entre si tais que 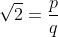 .Isto é,
.Isto é, 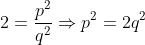 . Vamos supor, também, sem perda de generalidade, que
. Vamos supor, também, sem perda de generalidade, que  e
e  são positivos. Afirmamos que
são positivos. Afirmamos que  deve ser um número par: De fato, se
deve ser um número par: De fato, se  fosse da forma
fosse da forma 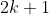 , então
, então (2k+1)&space;=&space;4k^2&space;+&space;4k&space;+1&space;=&space;2(2k^2&space;+&space;2k)+1) é impar, mas, como vimos,
é impar, mas, como vimos, 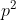 é par. Assim sendo, existe
é par. Assim sendo, existe 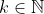 tal que
tal que 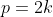 . Portanto,
. Portanto,  . De forma análoga a anterior, podemos concluir que
. De forma análoga a anterior, podemos concluir que  é par. Absurdo, pois
é par. Absurdo, pois  e
e  são primos entre si. Portanto, segue que
são primos entre si. Portanto, segue que  é irracional.
é irracional.
4. Decomposição de números naturais em fatores primos: Todo número natural ou é primo ou pode ser expresso como produto de fatores primos.
• Prova: Seja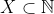 o conjunto dos números naturais não primos que não pode ser decomposto em fatores primos e suponhamos, por absurdo,
o conjunto dos números naturais não primos que não pode ser decomposto em fatores primos e suponhamos, por absurdo, 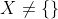 . Portanto, pelo Princípio da Boa Ordem,
. Portanto, pelo Princípio da Boa Ordem,  tem um menor elemento
tem um menor elemento 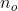 . Como
. Como 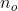 não é primo, por hipótese, existem
não é primo, por hipótese, existem 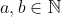 tais que
tais que 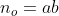 e a diferente de
e a diferente de 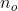 ou b diferente de
ou b diferente de 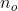 . Assim, teremos que
. Assim, teremos que 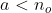 e
e 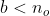 . Como
. Como 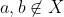 , existem
, existem 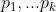 e
e 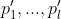 primos tais que
primos tais que 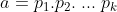 e
e 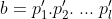 ou a ou b são primos (e a prova segue análoga, claramente). Portanto,
ou a ou b são primos (e a prova segue análoga, claramente). Portanto, 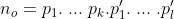 pode ser escrito como produto de fatores primos. Contradição. Portanto,
pode ser escrito como produto de fatores primos. Contradição. Portanto, 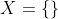 e segue que todo número natural é primo ou pode ser decomposto em produto de fatores primos.
e segue que todo número natural é primo ou pode ser decomposto em produto de fatores primos.
5. Infinitude dos números primos: (Euclides) Existem infinitos números primos
• Prova: Seja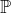 o conjunto dos números primos e suponhamos, por absurdo, que
o conjunto dos números primos e suponhamos, por absurdo, que 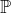 seja finito. Então,
seja finito. Então, 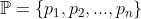 . Sendo assim, considere o número
. Sendo assim, considere o número 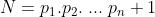 . Como
. Como 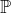 é finito,
é finito,  não é primo. Daí, segue que
não é primo. Daí, segue que  pode ser decomposto em fatores primos e, portanto, existe um
pode ser decomposto em fatores primos e, portanto, existe um 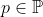 tal que
tal que  divide
divide  . Mas
. Mas  não é nenhum dos
não é nenhum dos 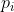 , pois, se o fosse, deveríamos ter que
, pois, se o fosse, deveríamos ter que  divide 1. Contradição. Portanto,
divide 1. Contradição. Portanto, 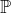 é infinito.
é infinito.
Bom, é isso. Apresentei algumas provas básicas que podem ser feitas desta maneira e entendidas por todos. Até hoje, utilizo muito a técnica mesmo em proposições que tratam de coisas menos básicas e esta é, de fato, muito útil em algumas situações. O único "mal" que podemos notar é que conclui-se, no meio do caminho, um monte de coisas falsas e chegamos num absurdo, ou seja, tudo o que foi concluído antes é, de certa forma, inútil para ser aproveitado em outras situações. Mas, ainda sim, esta continua sendo uma "técnica" válida e bem importante de provarmos algumas coisas.
Até
Algumas fontes importantes:
[1] Um curso de Análise vol. 1 - Elon Lages Lima
[2] Proofs from the book - Aigner e Ziegler
Neste tópico, vou expor algumas demonstrações feitas “por absurdo”, que foi uma das primeiras maneiras que eu aprendi a fazer demonstrações esse ano na faculdade. Além de objetivar o conhecimento da técnica, aos que gostariam de estudar matemática no futuro, vejamos um pouco mais da matemática "rigorosa" que será apresentada nos cursos, em geral.
Para os que não conhecem esta técnica (que tem ideia muito simples), ela consiste no seguinte: Suponhamos que temos uma proposição P1 que queremos provar ser verdadeira. Então supomos, por absurdo, que P1 seja falsa e chegar a um absurdo, ou seja, algo como 1=0 ou em alguma coisa que já sabemos que não é verdade. Claramente não é tudo que pode ser demonstrado por absurdo, devemos tomar cuidado para aplicar essa técnica para mostrarmos fatos que são ou não verdadeiros, e que a sua não falsidade implica que este é verdadeiro.
Certo, agora pode parecer um pouco confuso, mas vou mostrar alguns fatos básicos (e outros nem tanto) utilizando esta técnica e ficará mais claro. Vale ressaltar que demonstrações “por absurdo” ou “por contradição” são especialmente úteis quando queremos provar alguma coisa básica sem com que tenhamos muitas ferramentas ainda.
Vale a pena, para o total entendimento do tópico, a introdução de algumas definições e axiomas que, geralmente, não são conhecidos por alunos de ensino médio, mas que serão facilmente entendidos.
Os axiomas de Peano:
Seja
P1) A função s é injetiva. Ou seja, se
P2)
P3) (Princípio de Indução) Se
a)
b)
então
Bom, mostrar a existência de um conjunto que satisfaz essas características é um pouco mais difícil. Então vamos supor conhecido nosso conjunto de números naturais
Números primos: Dizemos que
Menor elemento: Seja
quando
Então vejamos algumas provas.
1. (Princípio da Boa Ordem) Todo subconjunto não vazio de números naturais tem um menor elemento.
• Prova: Seja
Se não, considere o conjunto
Com efeito, supondo, por absurdo, que
Então, segue que qualquer subconjunto não vazio de números naturais tem um menor elemento.
Bom, pode parecer que esse é um Teorema um pouco bobo, mas ele é bem útil visto que vamos usá-lo para provar, utilizando a técnica acima, o princípio de indução de uma forma mais parecido com a que conhecemos!
Definição: Dizemos que um subconjunto ordenado de números naturais satisfaz o Princípio da Boa Ordem se todos os seus subconjuntos têm um menor elemento.
2. O 2º Princípio de Indução: Seja
• Prova: Suponhamos, por absurdo, que
Portanto,
Bom, acredito que, agora, a ideia tenha ficado mais clara. Então vejamos mais algumas provas envolvendo outros temas. Esta é um clássico, provavelmente muitos já viram:
3. A irracionalidade de
Definição(1): Chamamos de raiz quadrada de um número real x, e denotamos por
Definição(2): Dizemos que um número real
• Prova: Suponhamos, por absurdo, que
4. Decomposição de números naturais em fatores primos: Todo número natural ou é primo ou pode ser expresso como produto de fatores primos.
• Prova: Seja
5. Infinitude dos números primos: (Euclides) Existem infinitos números primos
• Prova: Seja
Bom, é isso. Apresentei algumas provas básicas que podem ser feitas desta maneira e entendidas por todos. Até hoje, utilizo muito a técnica mesmo em proposições que tratam de coisas menos básicas e esta é, de fato, muito útil em algumas situações. O único "mal" que podemos notar é que conclui-se, no meio do caminho, um monte de coisas falsas e chegamos num absurdo, ou seja, tudo o que foi concluído antes é, de certa forma, inútil para ser aproveitado em outras situações. Mas, ainda sim, esta continua sendo uma "técnica" válida e bem importante de provarmos algumas coisas.
Até
Algumas fontes importantes:
[1] Um curso de Análise vol. 1 - Elon Lages Lima
[2] Proofs from the book - Aigner e Ziegler
Última edição por Giiovanna em Sáb 07 Dez 2013, 21:21, editado 1 vez(es)

Giiovanna- Grupo
Velhos amigos do Fórum
- Mensagens : 2128
Data de inscrição : 31/08/2012
Idade : 29
Localização : São Paulo, SP
 Re: Provas "por absurdo"
Re: Provas "por absurdo"
Bonito trabalho, Giiovanna, e muito útil também. Vou deixar como tópico fixo.
____________________________________________
In memoriam - Euclides faleceu na madrugada do dia 3 de Abril de 2018.

Lembre-se de que os vestibulares têm provas de Português também! Habitue-se a escrever corretamente em qualquer circunstância!
O Universo das coisas que eu não sei é incomensuravelmente maior do que o pacotinho de coisas que eu penso que sei.

Euclides- Fundador

- Mensagens : 32508
Data de inscrição : 07/07/2009
Idade : 74
Localização : São Paulo - SP
 Re: Provas "por absurdo"
Re: Provas "por absurdo"
Obrigada!  Se alguém tiver alguma dúvida ou quiser acrescentar alguma outra demonstração será bem vindo.
Se alguém tiver alguma dúvida ou quiser acrescentar alguma outra demonstração será bem vindo.

Giiovanna- Grupo
Velhos amigos do Fórum
- Mensagens : 2128
Data de inscrição : 31/08/2012
Idade : 29
Localização : São Paulo, SP
 Re: Provas "por absurdo"
Re: Provas "por absurdo"
Muito bom!

Wilson Calvin- Matador

- Mensagens : 524
Data de inscrição : 26/02/2013
Idade : 26
Localização : São Paulo
 Tópicos semelhantes
Tópicos semelhantes» Demonstração por absurdo
» lógica - redução ao absurdo
» Exercício de Logaritmo (Absurdo)
» Método de Redução ao Absurdo
» Explicação para um absurdo provado
» lógica - redução ao absurdo
» Exercício de Logaritmo (Absurdo)
» Método de Redução ao Absurdo
» Explicação para um absurdo provado
PiR2 :: Recursos extras :: Demonstrações
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos|
|
|













