Transformação de Radical Duplo

Acho que vcs conhecem a fórmula de transformação de radical duplo



Ela parece complicar as coisas, mas para cálculo de números complexos ela sempre facilita! Gostaria de saber se alguém conhece uma fórmula semelhante para os dois casos abaixo





Eu até encontrei isto


Mas não é bem o que eu esperava...

Obg!

RADICAL DUPLO:

Toda expressão irracional da forma: é denominada de RADICAL DUPLO.
A transformação de um radical duplo em muitas situações, para simplificar em muito o nosso cálculo com radicais, podemos transformar um radical duplo em uma soma algébrica de radicais simples, vejamos:

 
e para tal precisamos  que: e B não seja um quadrado perfeito.
Elevando cada membro dessa igualdade ao quadrado teremos:



Como cada membro dessa igualdade são formados por uma parte racional e outra irracional, elas podem ser isoladamente igualadas:

  e onde podemos concluir que:


Temos então a soma e o produto de dois números x e y, e com isso podemos montar uma equação do segundo grau:

 É fácil ver que:

Chamando

 , teremos

 e com isso:



Observemos que a diferença precisa ser, além de positiva, um quadrado perfeito. Só assim, conseguiremos, transformar um RADICAL DUPLO numa soma ou diferença de radicais simples. Notemos que é muito simplesinha essa equação e fácil de usa tanto nos reais como nos complexos.

Veremos agora um exemplo:

1) Transforme o radical duplo numa soma de radicais simples.

Notemos que:

é positivo e também um quadrado perfeito, portanto a transformação é possível,

assim:   e aplicando a transformação, vem:

   , portando usando raciocínio análogo você com certeza resolverá as outras questões.

                         Dyllway Carlos.

Dyllway Carlos, observe que a minha pergunta não é para o caso quadrático, e sim cúbico e quártico...

Entendo sua pergunta. Se você conhece,e pelo visto conhece e bem; o desenvolvimento para obter uma fórmula para os quadrados envolve a resolução de uma pequena equação de 2º grau, para o caso cúbico você obteu uma de terceiro, o que já era esperado. Se o que você fez estiver certo a equação para x de grau 3 não contém termo de x^2, assim ela pode ser resolvida pela substituição:
x=u+v
uv=-(a^2-b)^(1/3)

Pode substituir na infeliz equação resolver o sistema para x e y e encontrar o resultado (good lucky), é possível, mas te garanto que não encontrará nada bonito.

Para o caso quártico você pode reduzir a um caso quadrático duas vezes. 


 

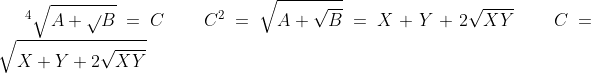
Onde estão as mesmas condições para o caso quadrático. Daqui a diante é a mesma história.

Jhenrique , a idéia nas expressões do tipo  é ter a noção de que  seja um produto notável . 

EX : 









Logo 

O único modo que eu conheço de resolver as do tipo  é deixando-a na forma  , aí você resolve o primeiro radical duplo e depois o segundo .

Acredito que a intensão do J Henrique seja encontrar um termo geral que resolva como no caso dos radicais quadráticos múltiplos.

Acredito que não exista fórmula para ambos os casos  .

Sim, a ideia é encontrar uma solução para



e para



Mas isso não é puro preciosismo matemático da minha parte, aqui tem até uma questão desse tipo que eu n sei como o autor resolve...

https://2img.net/r/ihimg/photo/my-images/547/qtrj.png/
fonte: http://pt.wikipedia.org/wiki/N%C3%BAmeros_complexos

Você se refere à solução da equação  Por Tartaglia:??

Eu conheço esse solução. Sei até mesmo deduzir todas as três raízes partindo da equação ax³+bx²+cx+d=0. Sei também calcular a raiz quadrada de um número complexo () sem precisar recorrer à forma trigonométrica. Para isto, eu utilizo a fórmula de transformação de arco duplo. Mas eu não sei calcular a raiz cúbica de um número complexo () sem apelar à forma trigonométrica, não sei pq não sei a sua fórmula de transformação de arco duplo para este caso. E o que eu gostaria de saber é fazer isto, calcular as raízes cúbicas ou quárticas (ou seja, determinar os coeficientes a e b) de um número complexo sem precisar recorrer a arredondamentos trigonométricos.

(ps: já que tocamos no assunto da resolução da cúbica, a resolução da quártica é uma outra coisa que infelizmente eu desconheço e que eu gostaria de poder compreender melhor...)