Pares ordenados (x,y)

por **Pietro di Bernadone** Ter 19 Mar 2013, 20:38

O lugar geométrico dos pares ordenados 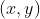$Pares ordenados (x,y) Gif$ que satisfazem a igualdade 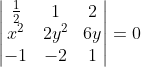$Pares ordenados (x,y) Gif$ é um (a)

a) ponto

b) par de retas paralelas

c) circunferência de raio 3

d) par de retas perpendiculares

e) circunferência de centro (1,2)

por Dinheirow Ter 19 Mar 2013, 22:14

Calculando o determinante
y² - 6y - 4x² + 4y² + 6y - x² = 0
5y² - 5x² = 0
y² = x² daqui, extraindo-se a raíz temos que y = ± x
correspondente às retas perpendiculares y = x e y = -x
letra d

por **Pietro di Bernadone** Ter 19 Mar 2013, 22:51

Boa noite Dinheirow,

também encontrei y = ± x. A partir daí não consegui enxergar que as retas são perpendiculares!

Pode me ajudar?

por **JoaoGabriel** Ter 19 Mar 2013, 23:28

Considere retas y = mx + n e y' = ax + b:

Condição de perpendicularidade: o produto dos coeficientes angulares deve ser -1.

No caso, m*a = -1

É o que ocorre para y = x e y = - x

1*(-1) = -1

por **Pietro di Bernadone** Qua 20 Mar 2013, 10:43

Bom dia João,

entendi sua explicação! Apenas para quetões de conhecimento: A perpendicularidade das retas y = x e y' = -x acontece na origem (0,0), não é mesmo?

Obrigado,

Pietro

por **JoaoGabriel** Qua 20 Mar 2013, 11:12

Pietro di Bernadone escreveu:Bom dia João,

entendi sua explicação! Apenas para quetões de conhecimento: A perpendicularidade das retas y = x e y' = -x acontece na origem (0,0), não é mesmo?

Obrigado,

Pietro

Perfeitamente, a origem é o único ponto de encontro das funções:

Pares ordenados (x,y) Image