Equação Polinomial

por Man Utd 25/10/2012, 9:08 pm

A equação x^4-3x^2+px+q=0(p e q coeficientes reais) tem duas raízes complexas cuja soma é -6 e cujo produto é 25.As raízes reais desse polinômio são tais qye uma é o dobro da outra.

a)obtenha as quatro raízes da equação.

b)Determine p e q.

Spoiler:

por **JoaoGabriel** 25/10/2012, 9:38 pm

O polinômio dado possui 4 raízes, sendo (de acordo com o enunciado) 2 reais e 2 complexas. O fato de 2 raízes serem complexas levá-nos à conclusão que uma é o conjugado da outra.

Considere as raízes nas formas a + bi e a - bi

A soma destas raízes é -6 e o produto é 25. Usemos isto:

$\\a+bi+a-bi=-6\to a=-3\\\\(a+bi)(a-bi)=25 \therefore a^2 + b^2 = 25\to 9 + b^2 = 25 \to b = \pm 4$

As raízes complexas então ficam:

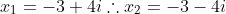
$\\x_1 = -3 + 4i \therefore x_2 = -3 - 4i$

Agora tratando das raízes reais (x3 e x4), temos a seguinte relação:

$\\x_4 = 2x_3$

Pelas relações de Girard:

$\\S = 0 \therefore -6 + x_3 + 2x_3 = 0\to x_3 = 2 \therefore x_4 = 4$

Pela outra relação (produto das raízes):

$\\(-3-4i)(-3+4i)8 = q \therefore 25.8 = q\to q = 200$

Substituindo x = 2 na equação para determinar P:

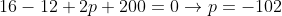
$\\16 -12+2p+200 = 0 \to p = -102$

é isso aê, abração Very Happy

por Man Utd 26/10/2012, 8:58 am

vlw mano gostei muito da sua resolução,a resolução do livro era muito complicada,obrigado msm abraços!! Very Happy

por Conteúdo patrocinado

Equação Polinomial

Equação Polinomial

Re: Equação Polinomial

Re: Equação Polinomial

Re: Equação Polinomial

Um fórum livre e democrático.