Polígonos Regulares

1) Um trapézio está inscrito em um círculo de raio 4 cm. Determine a altura do trapézio, sabendo que suas bases são respectivamente o lado do triângulo equilátero e o lado do hexágono regular inscritos nesse círculo.

R: 2(V3 + 1)cm ou 2(V3 - 1) cm

2)

3)

Giovane

Por favor leia o Regulamento do fórum, no alto desta página.
Ele contém as Regras do fórum, a serem seguidas por todos os usários.
Você transgrediu a Regra X I. Vou apagar as questões 2 r 3
Por favor sigas as regras nas próximas postagens

Desenhe um trapézio isósceles inscrito num círculo de centro O.
Una os vértices ao centro, Sejam AB a base maior e CD a base menor

Lado do triângulo isóscles (base maior) ----> AB = 2*(R*cos30º) ----> AB = 2*4*\/3/2 ----> AB = 4*\/3

Lado do hexágono regular (base menor) ----> CD = R ----> CD = 4

Altura h do triângulo CDO em relação à CD ----> h = R*cos30º ----> h = 2*\/3

Altura h' do triângulo ABO em relação à AB ----> h' = R*cos60º ----> h' = 2

Altura do trapézio ----> H = h + h' ----> H = 2*\/3 + 2 ----> H = 2*(\/3 + 1)

Não consigo visualizar a solução 2*(\/3 - 1)

Desculpe-me pela transgressão. Obrigado pelo aviso e pela solução.

Um abraço

[IMG]https://2img.net/h/oi48.tinypic.com/2w2rk1l.png[/IMG

Outra opção.
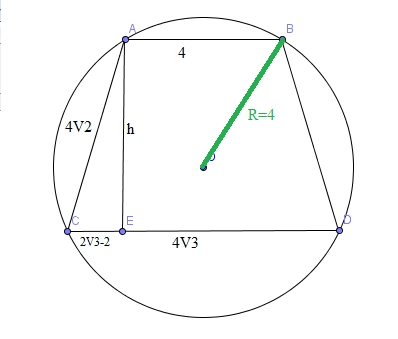
AB - lado do hexágono inscrito AB=4 , subentende um arco de 60°
CD - lado do triângulo equilátero inscrito CD=4V3 subentende arco de 120°
Sendo as bases do trapézio paralelas , concluímos que esses lados não paralelos subtendem arcos de 90° cada um, ou seja ,o lado de um quadrado que mede 4V2.
Concluímos também que o trapézio é isósceles.

Aplicando Pitagoras no triângulo ACE temos: h²=(4V2)2 - (2V3-2)²
h²=16-8V3
h²=± V4(4-2V3)>>>h=± (V3-1)² >>>h=± 2(V3-1)
Lembrando que:

(V3-1)² = 3-2V3+1 = 4 - 2V3

Obrigado Raimundo. Um abraço.

:bball: