Cônicas e órbitas

Suponha que você esteja navegando pelo universo quando decide medir a distância entre 2 estrelas: A1 e A2. Você se aproxima da A1 de forma que seja atraído gravitacionalmente e comece a orbitá-la. Se a sua velocidade enquanto estava livre de influências gravitacionais era V0 = 20,0km/s e no ponto de máxima aproximação com A1 a distância até a estrela era de d = 0,15UA, calcule:

a) O formato da órbita 
b) O semieixo maior (a) e a metade da distância entre os focos (c) dessa órbita. Você esperou para tirar uma foto da estrela A2 sempre que a distância de você até a A1 fosse igual a c, e calculou a diferença angular entre as posições da estrela nas duas fotos com relação às estrelas distantes. Tal valor foi de θ = 0,04”. 
c) Calcule a distância entre as duas estrelas. Dados: massa de A1 MA1 = MSol = 1,989 · 10^30 kg . Considere também que A2 está sobre a linha que liga você até A1 durante a máxima aproximação. 

Não consigo resolver 

Gab:

a) Hipérbole 
b) a = 2,217UA e c = 2,37UA 
c) d = 67,6pc

Vamos partir da premissa de que a estrela \(A_1\) não possui planetas, de forma que o sistema nave-estrela seja um problema clássico dois corpos, livre da interferência gravitacional de outros objetos.

Nessa configuração, excetuando-se o caso de colisão, nunca haverá a captura gravitacional da nave pela estrela, cortesia da conservação da energia,
\[(K+U)_\text{i}=(K+U)_\text{f}\]
sendo \(K\) é a energia cinética da nave e \(U\) a energia potencial gravitacional (que é negativa).
\[\frac{1}{2}mv_\infty^2=\frac{1}{2}mv^2-\frac{GMm}{r}\]
Onde \(m\) é a massa da nave, \(v_\infty\) a velocidade antes da entrada no sistema, \(v\) a velocidade da nave quando ela está sob a influência gravitacional da estrela, \(G\) a constante gravitacional universal, \(M\) a massa da estrela e \(r\) a distância entre a nave e a estrela no periastro.
\[v_\infty^2=v^2-\frac{2GM}{r}\]
Para que a energia seja conservada, a velocidade \(v\) aumenta na medida em que a nave fica mais próxima da estrela.

Dessa maneira, não importa o quão próxima a nave esteja da estrela, ela não é capturada.

Assim, a nave passa pela estrela por uma trajetória aberta - hiperbólica -, com a estrela posicionada no foco da hipérbole.

A entrada em órbita permanente ao redor da estrela - órbita elíptica e fechada - requer que a nave utilize algum tipo de mecanismo de propulsão para conduzir as manobras de redução a velocidade e alteração direção do deslocamento.


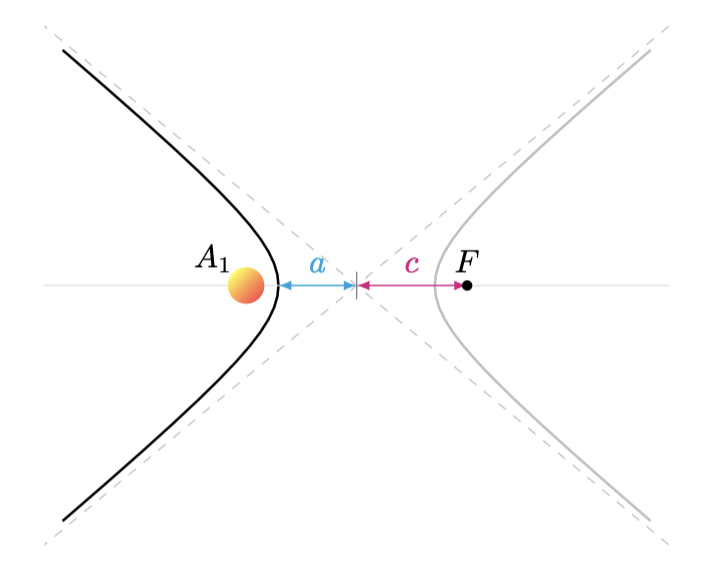
O trecho direito da hipérbole não possui sentido físico, apenas simetria matemática em relação ao lado esquerdo, que é a trajetória percorrida pela nave.

Agora podemos calcular os parâmetros geométricos da curva em função dos observáveis físicos.

A distância \(a\) é dada por
\[a=\frac{GM}{v_\infty^2}=\frac{6,\!67\times 10^{-11}\cdot1,\!989\times 10^{30}}{(2\times 10^4)^2}\]
\[a\simeq3,\!317\times 10^{11}~\text{m}\]
Para transformar esse valor em unidades astronômicas, basta dividi-lo por \(1~\text{ua}=1,\!496\times 10^{11}~\text{m}\), obtendo assim
\[\color{red} a\simeq 2,\!217~\text{ua}\]
O parâmetro \(c\) é calculado a partir de \(a\) e da distância de maior aproximação \(r\).
\[c=a+r\]
\[c=a+0,\!15~\text{ua}\]
Como temos \(a\) em \text{ua}, podemos calcular \(c\) diretamente nessa unidade.
\[c\simeq 2,\!217+0,\!15\]
\[\color{red} c\simeq 2,\!367~\text{ua}\]

Aparentemente, seria esperado que a resposta para o item (c) fosse calculada por paralaxe estelar, mas não cheguei ao número de 67,6 pc.

Seja como for, deixo aqui os meus cálculos e um diagrama que reflete o meu entendimento sobre o problema.

Pelo triângulo,
\[\tan \theta = \frac{c}{d}\]
\[d=\frac{c}{\tan \theta}=\frac{3,\!541\times 10^{11}}{\tan {0,\!04}''}\]
\[d=1,\!826\times 10^{18}~\text{m}\]
Um parsec é equivalente a \(3,\!09\times 10^{16}~\text{m}\).
\[\color{red} d\simeq 59,2~\text{pc}\]
Por esse caminho, a resposta esperada \(d=67,\!6~\text{pc}\) dependeria de um cateto maior que \(c\) ou do ângulo de paralaxe um pouco menor: \(\theta={0,\!035}''\).

Materiais interessantes sobre os temas tratados no exercício:
https://venautics.space/en/complement-2/bases-of-the-mechanical-orbital/3-trajectory-hyperbolic/
https://www.quora.com/How-close-would-an-asteroid-have-to-pass-to-get-pulled-into-orbit-around-the-Earth