equações trigonométricas

Obtendo as soluções da equação sen(x) +  √3 cos(x) = 1, x ∈ [0,2π], conclui-se que a soma dessas soluções é igual a 

resp: 7π/3 rad

[latex]\sin(x)+\sqrt{3}\cos(x)=1 \iff  1\cdot\sin(x)+\sqrt{3}\cos(x)=1[/latex]

Temos que [latex]\sqrt{1^2+(\sqrt{3})^2 }= 2 [/latex], portanto dividindo por 2:


    [latex]\sin(x)+\sqrt{3}\cos(x)=1 \iff  \dfrac{1}{2}\cdot \sin(x) +\dfrac{\sqrt{3}}{2} \cdot \cos(x) = \dfrac{1}{2}[/latex]

Observe que [latex]\cos\left(\dfrac{\pi}{3}\right) = \dfrac{1}{2}[/latex] e que [latex]\sin\left(\dfrac{\pi}{3}\right) = \dfrac{\sqrt{3}}{2}[/latex]:

[latex]\sin(x)+\sqrt{3}\cos(x)=1 \iff \cos\left(\dfrac{\pi}{3}\right) \cdot \sin(x) +\sin\left(\dfrac{\pi}{3}\right) \cdot \cos(x) = \dfrac{1}{2} \iff \sin\left(\dfrac{\pi}{3}+x\right) = \dfrac{1}{2}[/latex]



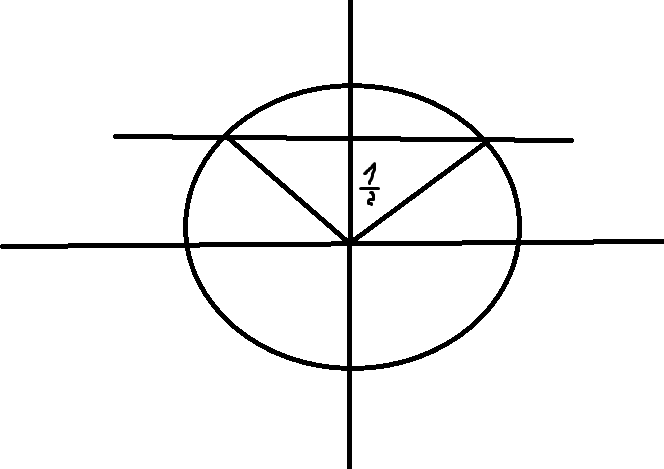
No domínio, há 2 valores possíveis para x: pi/2, 11pi/6 (2pi-pi/6) .

Somando dá pi/2+11pi/6 = 14pi/6 = 7pi/3

\[
\begin{align*}
\Big( \sin(x) + \sqrt{3} \cos(x) & = 1 \Big) \cdot \left( \sin(x) - \sqrt{3} \cos(x) \right) \\
\sin^2(x) - 3 \cos^2(x) & = \sin(x) - \underbrace{\sqrt{3} \cos(x)}_{1-\sin(x)} \\
\sin^2(x) - 3 ( 1 - \sin^2(x) ) & = \sin(x) - 1 + \sin(x) \\
4\sin^2(x) - 3 & = 2 \sin(x) -1 \\
4\sin^2(x) -2\sin(x) - 2 & = 0  \\
\end{align*}
\]
Resolvendo a equação de segundo grau em \( \sin(x) \):
\[
\begin{align*}
\sin(x) & = \frac{1 \pm \sqrt{ 1 + 8} }{4} \\
& = \frac{1 \pm 3 }{ 4 } \\
\end{align*}
\]
Assim,
\[
\sin(x) = \frac{1 + 3 }{4} = 1 \Leftrightarrow x = \frac{\pi}{2} \quad \land \quad \sin(x) = \frac{1 - 3}{4} = - \frac{1}{2} \Leftrightarrow x = \left\{ \frac{7\pi}{6} , \frac{11\pi}{6} \right\}
\]
Avaliando as raízes encontradas, \( x = \frac{7\pi}{6} \) não procede, de modo que a soma das raízes é \( S = \frac{\pi}{2} + \frac{11\pi}{6} = \frac{7\pi}{3} \).

Outro método:

https://pir2.forumeiros.com/t150465-o-truque-do-triangulo-retangulo