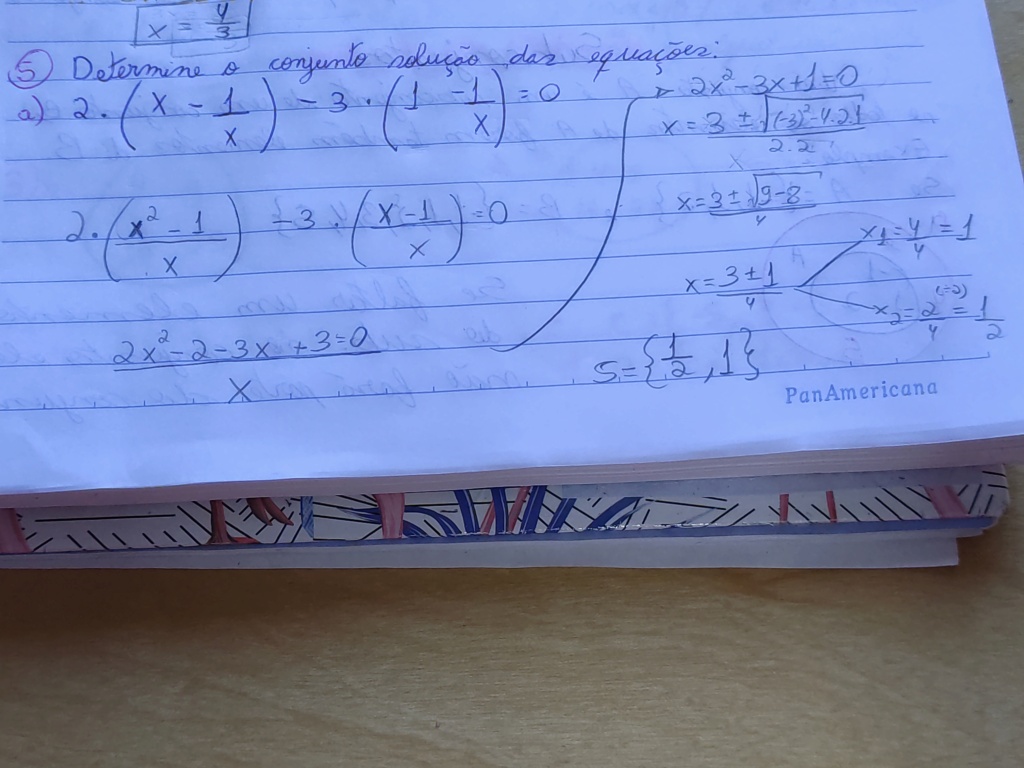Equação do 2° grau
4 participantes
Página 1 de 1

Medeiros- Grupo
Velhos amigos do Fórum
- Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
imAstucia gosta desta mensagem
 Re: Equação do 2° grau
Re: Equação do 2° grau
2(x - 1/x) - 3(1 - 1/x) = 0 [multiplique os denominadores e os numeradores de x e 1 por x; não alterará seus valores (de fato, x·x/x = x e 1·x/x = 1]
2(x²/x - 1/x) - 3(x/x - 1/x) = 0 [frações com o mesmo denominador: some (subtraía) os numeradores e mantenha o denominador]
2((x² - 1)/x) - 3((x - 1)/x) = 0 [multiplicando ambos os membros da equação por x irá o 'eliminar' nos denominadores]
2x² - 2 - 3x + 3 = 0 [propriedade distributiva da multiplicação]
2x² - 3x + 1 = 0 [a (coef. de x²) = 2; b (coef. de x) = -3; c = 1)
∆ = b² - 4ac = 9 - 8 = 1
x = (- b ± √∆)/2a
x = (3 ± 1)/4 [-(-3) = 3; √1 = 1]
x = 1 ou x = 1/2
S = {x ∈ ℝ / x = 1 ou x = 1/2}
2(x²/x - 1/x) - 3(x/x - 1/x) = 0 [frações com o mesmo denominador: some (subtraía) os numeradores e mantenha o denominador]
2((x² - 1)/x) - 3((x - 1)/x) = 0 [multiplicando ambos os membros da equação por x irá o 'eliminar' nos denominadores]
2x² - 2 - 3x + 3 = 0 [propriedade distributiva da multiplicação]
2x² - 3x + 1 = 0 [a (coef. de x²) = 2; b (coef. de x) = -3; c = 1)
∆ = b² - 4ac = 9 - 8 = 1
x = (- b ± √∆)/2a
x = (3 ± 1)/4 [-(-3) = 3; √1 = 1]
x = 1 ou x = 1/2
S = {x ∈ ℝ / x = 1 ou x = 1/2}
LucasCord- Iniciante
- Mensagens : 20
Data de inscrição : 13/01/2022
imAstucia gosta desta mensagem
Arianacarolina- Recebeu o sabre de luz

- Mensagens : 118
Data de inscrição : 04/01/2021
 Re: Equação do 2° grau
Re: Equação do 2° grau
Restrição --> x ≠ 0
2.(x - 1/x) - 3.(1 - 1/x) = 0
2.(x - 1/x) - 3.(x/x - 1/x) = 0
2.(x² - 1)/x - 3.(x - 1)/x ---> *x
2.(x² - 1) - 3.(x - 1) = 0
2.(x - 1).(x +1) - 3.(x - 1) = 0 ---> (x - 1) em evidência:
(x - 1).[2(x + 1) - 3] = 0
(x - 1).(2.x - 1) = 0
x = 1 e x = 1/2
2.(x - 1/x) - 3.(1 - 1/x) = 0
2.(x - 1/x) - 3.(x/x - 1/x) = 0
2.(x² - 1)/x - 3.(x - 1)/x ---> *x
2.(x² - 1) - 3.(x - 1) = 0
2.(x - 1).(x +1) - 3.(x - 1) = 0 ---> (x - 1) em evidência:
(x - 1).[2(x + 1) - 3] = 0
(x - 1).(2.x - 1) = 0
x = 1 e x = 1/2

Elcioschin- Grande Mestre

- Mensagens : 73164
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Arianacarolina gosta desta mensagem
 Re: Equação do 2° grau
Re: Equação do 2° grau
Arianacarolina escreveu:Acredito que a resolução correta seja essa:
Não entendi como o senhor resolveu essa questão, porque só consegui atingir essa resolução :
Carolina
Eu ERREI. Foi falta de atenç˜ao minha, considerei os dois parˆenteses como sendo iguais -- o colega Lucas, na sequˆencia, percebeu isso e negritou a diferença.
Em resumo, a resposta que dei n˜ao se refere ao exerc´icio que vocˆe postou.

Medeiros- Grupo
Velhos amigos do Fórum
- Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
 Tópicos semelhantes
Tópicos semelhantes» Equação 2° Grau
» Equação do 2 grau II
» Equação 2 grau
» Equação de 2° Grau
» Equação do 2º grau - 21
» Equação do 2 grau II
» Equação 2 grau
» Equação de 2° Grau
» Equação do 2º grau - 21
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos