Função Logarítmica
2 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Função Logarítmica
por abelardo Qua 28 Set 2011, 10:23
Com relação a função real definida por =\log_{2}(1-x^2) "f(x)=\log_{2}(1-x^2)")
de 
em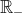 
, considere as afirmações:
I) f(x) é sobrejetora.
II) f(x) é uma função par.
III)<f\left ( \frac{-1}{2} \right ) "f\left ( \frac{7}{8} \right )<f\left ( \frac{-1}{2} \right )")
Todas estão corretas. As letras b) e c) eu fiz, mas como seria uma solução analítica para a letra a)?
I) f(x) é sobrejetora.
II) f(x) é uma função par.
III)
Todas estão corretas. As letras b) e c) eu fiz, mas como seria uma solução analítica para a letra a)?
abelardo- Grupo
Velhos amigos do Fórum
- Mensagens : 777
Data de inscrição : 12/03/2011
Idade : 32
Localização : Sertânia, Pernambuco, Brasil
Re: Função Logarítmica
por rihan Sáb 01 Out 2011, 01:18
Função Sobrejetora:= o Codomínio(f) é também a Imagem(f).
Todo o conjunto de chegada tem que ter correspondente no de partida.
O domínio é o intervalo aberto (-1;1), o CD são os reais não positivos.
Basta você verificar se a Imagem também são os reais não positivos.
Quando x= 0 temos f(0) = 0
Quando x < 0 temos f(x) < 0
Quando x → -1 temos f(x) → -∞
Quando x > 0 temos f(x) < 0
Quando x → +1 temos f(x) → -∞
Então quando passeamos x de algo maior que -1 até algo menor do que +1 a imagem percorre todos os reais não positivos, até demais: 2 vezes ! :cyclops: :cyclops:
Logo a Imagem coincide com o CD, então:
f(x) é sobrejetora.
E vamos lá !
Saudações bijetoras !
Todo o conjunto de chegada tem que ter correspondente no de partida.
O domínio é o intervalo aberto (-1;1), o CD são os reais não positivos.
Basta você verificar se a Imagem também são os reais não positivos.
Quando x= 0 temos f(0) = 0
Quando x < 0 temos f(x) < 0
Quando x → -1 temos f(x) → -∞
Quando x > 0 temos f(x) < 0
Quando x → +1 temos f(x) → -∞
Então quando passeamos x de algo maior que -1 até algo menor do que +1 a imagem percorre todos os reais não positivos, até demais: 2 vezes ! :cyclops: :cyclops:
Logo a Imagem coincide com o CD, então:
f(x) é sobrejetora.
E vamos lá !
Saudações bijetoras !
rihan- Estrela Dourada
- Mensagens : 5049
Data de inscrição : 22/08/2011
Idade : 69
Localização : Rio de Janeiro, RJ, Itabuna-Ilhéus, BA, Brasil
Tópicos semelhantes» Matemática: função exponencial e função logarítmica
» Função logaritmica e função exponencial (teórica).
» Função logarítmica
» Função Logarítmica
» Função logarítmica[2]
» Função logaritmica e função exponencial (teórica).
» Função logarítmica
» Função Logarítmica
» Função logarítmica[2]
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
